Introduction

This project implements a text encryption and decryption system using a matrix-based encryption technique. This project serves as an educational and practical exploration of matrix-based encryption techniques, demonstrating the fundamental concepts of encryption and decryption in a user-friendly manner.

How to implement this Library

Clone the repository and copy the library your local project folder then include MatrixEncryptor.h. After that you need to implement Eigen to your project. From the given link, only the folder Eigen is required. After putting it to your project folder, from your Project's Property Pages, C/C++ -> General -> Additional Include Directories add Eigen folder's path.

Getting started

Prerequisites

Before getting started with Text Encryption With Linear Algebra, ensure that you have the following dependencies installed on your Linux system:

• g++ compiler
• Eigen library

Installation

To use the Text Encryption With Linear Algebra, follow these steps:

1. Clone this repository

git clone git@github.com:farukalpay/TextEncryptionWithLinearAlgebra.git

2. Clone the repository of Eigen Library:

git clone https://gitlab.com/libeigen/eigen

3. Go inside the directory of Eigen Library and copy the directory Eigen into this repository

cp -r <path-to-Eigen-directory> <path-to-this-repo>

4. Use the Makefile to compile with make

make

5. Now you should see the executable in the directory of Text Encryption With Linear Algebra

Explanation of the Algorithm

Convert Input String to ASCII Integer

1. Initialization:

   • Given an input string $S$ of length $n$, where $S=s_1{s}_2{s}_3\dots s_n$, and each $s_i$ represents a character in the string.
     Initialize an empty vector $\text{parsed}$ to store the ASCII integer representations of characters extracted from the input string $S$.

   • Consider the input string $S=\text{"Hello World"}$.
     Initialize $\text{parsed}=[]$.

2. Token Extraction:

   • Extract tokens (words) from the input string $S$. Let $T_1,T_2,\dots ,T_m$ be the tokens extracted from $S$, where $m$ is the number of tokens.

   • Extract tokens: $T_1=\text{"Hello"}$ and $T_2=\text{"World"}$.

3. Character Processing for Token $T_i$:

   • For each token $T_i$, consisting of characters $t_{i1},t_{i2},\dots ,t_{ik}$, where $k$ is the length of the token:

     • Convert each character $t_{ij}$ to its ASCII integer representation $a_{ij}$.
     • Add each $a_{ij}$ to end of the $parsed$ vector.

   • Convert 'H' to ASCII integer $72$, 'e' to $101$, 'l' to $108$, 'l' to $108$, 'o' to $111$.
     Add these integers to $\text{parsed}$: $[72,101,108,108,111]$.

4. Adding Space:

   • After processing each character in a token $T_i$, add a space character ' ' to the $parsed$ vector.

   • Add a space ' ' to $\text{parsed}$.

5. End of Token:

   • Repeat steps 3-4 for all tokens $T_1,T_2,\dots ,T_m$.

   • Process characters for $T_2$:

     • Convert 'W' to ASCII integer $87$, 'o' to $111$, 'r' to $114$, 'l' to $108$, 'd' to $100$.
     • Add these integers to $\text{parsed}$: $[87,111,114,108,100]$.
     • Add a space ' ' to $\text{parsed}$.

6. Return Result:

   • The function returns the $\text{parsed}$ vector containing ASCII integer representations of characters in $S$, with spaces after each token.

   • Return $\text{parsed}=[72,101,108,108,111,32,87,111,114,108,100,32]$.

Generate Random Key

1. Initialization:

   • Let $key$ be a square matrix of size $size\times size$, represented as $key=[ke{y}_{ij}]$ where $i,j=0,1,\dots ,size-1$.

   • Each element $ke{y}_{ij}$ denotes a value in the key matrix.

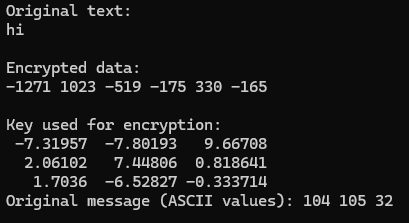
   • Consider the ASCII representation of the string $\text{"hi"}+\text{Space (ASCII 32)}$, where the ASCII values are $[104,105,32]$. Let $key$ be a square matrix of size $3\times 3$

2. Random Number Generation Setup:

   • Initialize a pseudo-random number generator with a random seed.

3. Uniform Distribution Setup:

   • Define a uniform distribution to produce random numbers uniformly distributed between -10.0 and 10.0.

4. Random Key Generation:

   • For each element $ke{y}_{ij}$ of $key$:
     • Sample a random value $r_{ij}$ from the uniform distribution.
     • Assign $r_{ij}$ as the value of $ke{y}_{ij}$ in the key matrix.
     • Mathematically, $ke{y}_{ij}=r_{ij}$ for $i,j=0,1,\dots ,size-1$.

5. Return the Key:

   • Once all elements of the matrix $key$ have been assigned random values, return the resulting key matrix $key$.

   • Generated key matrix for $[104,105,32]$:

$$\text{K}=\left[\begin{array}{ccc}1.25024& -2.33247& -3.94038\\ 3.39427& 0.800577& -5.14653\\ -6.62477& -1.65797& 3.84418\end{array}\right]$$

Encryption Algorithm

1. Message Padding:

   • Given a message $M$ represented as a vector of integers $\text{message}=[m_1,m_2,\dots ,m_n]$, where $n$ is the size of the message and $\text{size}$ is the size of the key matrix.

   • Determine the remainder $r$ when dividing the size of the message by the size of the key matrix: $r=\text{size}-(n\mathrm{mod}\text{size})$.

   • Pad the message with spaces to make its size a multiple of the size of the key matrix: $M^{\prime }=[m_1,m_2,\dots ,m_n,\underset{r\text{ times}}{\underbrace{\text{space},\text{space},\dots ,\text{space}}}]$.

   • The message $\text{"hi"}$ corresponds to the vector $\text{message}=[104,105,32]$. Since the size of the key matrix is 3, the message needs to be padded with spaces to make its size a multiple of $3$. Thus, the padded message becomes $[104,105,32,32,32,32]$.

2. Message Vectorization:

   • Split the padded message $M^{\prime }$ into vectors of size $\text{size}$: ${\text{messageVector}}_1,{\text{messageVector}}_2,\dots ,{\text{messageVector}}_k$, where $k=\frac{n+r}{\text{size}}$.

   • Each ${\text{messageVector}}_i$ is a column vector of size $\text{size}$ containing consecutive elements from $M^{\prime }$.

   • Generated ${\text{messageVector}}_i$ column matrices for $[104,105,32,32,32,32]$:

$${\text{messageVector}}_1=\left[\begin{array}{c}104\\ 105\\ 32\end{array}\right],{\text{messageVector}}_2=\left[\begin{array}{c}32\\ 32\\ 32\end{array}\right]$$

3. Encryption:

   • For each message vector ${\text{messageVector}}_i$:
     • Perform matrix-vector multiplication with the key matrix $K$: ${\text{encryptedVector}}_i=K\cdot {\text{messageVector}}_i$.
     • After performing the matrix-vector multiplication, the resulting elements in ${\text{encryptedVector}}_i$ rounded to the nearest integer.
     • Each element of ${\text{encryptedVector}}_i$ represents an encrypted value corresponding to the corresponding message vector element.

For ${\text{messageVector}}_1$:

$${\text{encryptedVector}}_1=K\cdot {\text{messageVector}}_1=\left[\begin{array}{ccc}1.25024& -2.33247& -3.94038\\ 3.39427& 0.800577& -5.14653\\ -6.62477& -1.65797& 3.84418\end{array}\right]\left[\begin{array}{c}104\\ 105\\ 32\end{array}\right]=\left[\begin{array}{c}-(int+round)240.97655\\ (int+round)272.375705\\ -(int+round)740.04917\end{array}\right]=\left[\begin{array}{c}-241\\ 272\\ -740\end{array}\right]$$

For ${\text{messageVector}}_2$:

$${\text{encryptedVector}}_2=K\cdot {\text{messageVector}}_2=\left[\begin{array}{ccc}1.25024& -2.33247& -3.94038\\ 3.39427& 0.800577& -5.14653\\ -6.62477& -1.65797& 3.84418\end{array}\right]\left[\begin{array}{c}32\\ 32\\ 32\end{array}\right]=\left[\begin{array}{c}-(int+round)160.72352\\ -(int+round)30.453856\\ -(int+round)142.03392\end{array}\right]=\left[\begin{array}{c}-161\\ -30\\ -142\end{array}\right]$$

4. Result:

   • Concatenate all elements of the encrypted vectors to form the encrypted message $E$: $E=[{\text{encryptedVector}}_1[1],{\text{encryptedVector}}_1[2],\dots ,{\text{encryptedVector}}_k[\text{size}],\dots ]$.

   • The resulting encrypted message corresponding to the input $\text{"hi"}$ encrypted using this key matrix is:

$$\text{E = [-241, 272, -740, -161, -30, -142]}$$

Decryption Algorithm

1. Initialization:

   • Let $\text{EncryptedMessage}=[e_1,e_2,\dots ,e_n]$ be the encrypted message represented as a vector of integers, where $n$ is the size of the encrypted message.

   • Consider the encrypted message $E=[-241,272,-740,-161,-30,-142]$

   • Key matrix $K$ used for encryption:

$$\text{K}=\left[\begin{array}{ccc}1.25024& -2.33247& -3.94038\\ 3.39427& 0.800577& -5.14653\\ -6.62477& -1.65797& 3.84418\end{array}\right]$$

2. Segmentation:

   • Divide the encrypted message into segments, each consisting of $\text{size}$ elements, where $\text{size}$ is the size of the key matrix $K$.

   • Segments of the encrypted message, denoted as ${\text{Segment}}_i$, are obtained by splitting $\text{EncryptedMessage}$ into $\frac{n}{\text{size}}$ segments, where $i$ ranges from $1$ to $\frac{n}{\text{size}}$.

   • Each segment ${\text{Segment}}_i$ consists of $\text{size}$ consecutive elements starting from index $i\times \text{size}$.

   • Each segment ${\text{Segment}}_i$ is represented as a column matrix of size $\text{size}$:

$${\text{Segment}}_i=\left[\begin{array}{c}{e}_{(i-1)\times \text{size}+1}\\ e_{(i-1)\times \text{size}+2}\\ ⋮\\ e_{i\times \text{size}}\end{array}\right]$$

• Segmented column matrices for $E=[-241,272,-740,-161,-30,-142]$:

$${\text{EncryptedVector}}_1=\left[\begin{array}{c}-241\\ 272\\ -740\end{array}\right],{\text{EncryptedVector}}_2=\left[\begin{array}{c}-161\\ -30\\ -142\end{array}\right]$$

3. Matrix Multiplication:

   • For each segment ${\text{encryptedVector}}_i$:
     • Perform matrix-vector multiplication with the inverse key matrix $K^{-1}$: ${\text{decryptedVector}}_i=K^{-1}\cdot {\text{encryptedVector}}_i$
     • After performing the matrix-vector multiplication, the resulting elements in ${\text{decryptedVector}}_i$ rounded to the nearest integer.
     • Each element of ${\text{decryptedVector}}_i$ represents an decrypted ASCII value corresponding to the corresponding message vector element.

For ${\text{encryptedVector}}_1$:

$${\text{decryptedVector}}_1=K^{-1}\cdot {\text{encryptedVector}}_1=\left[\begin{array}{ccc}0.09985& -0.28369& -0.27745\\ -0.38522& 0.38983& 0.12703\\ 0.00592& -0.32077& -0.16323\end{array}\right]\left[\begin{array}{c}-241\\ 272\\ -740\end{array}\right]=\left[\begin{array}{c}(int+round)104.09060\\ (int+round)104.86881\\ (int+round)32.11234\end{array}\right]=\left[\begin{array}{c}104\\ 105\\ 32\end{array}\right]$$

For ${\text{encryptedVector}}_2$:

$${\text{decryptedVector}}_2=K^{-1}\cdot {\text{encryptedVector}}_2=\left[\begin{array}{ccc}0.09985& -0.28369& -0.27745\\ -0.38522& 0.38983& 0.12703\\ 0.00592& -0.32077& -0.16323\end{array}\right]\left[\begin{array}{c}-161\\ -30\\ -142\end{array}\right]=\left[\begin{array}{c}(int+round)31.83422\\ (int+round)32.28774\\ (int+round)31.84724\end{array}\right]=\left[\begin{array}{c}32\\ 32\\ 32\end{array}\right]$$

5. Result:

   • Concatenate all elements of the decrypted message vectors to form the decrypted message $D$: $D=[{\text{decryptedVector}}_1[1],{\text{decryptedVector}}_1[2],\dots ,{\text{decryptedVector}}_k[\text{size}],\dots ]$. The resulting decrypted message is a sequence of ASCII characters obtained by converting each integer in $D$ to its corresponding ASCII character.

   • The resulting decrypted message corresponding to the encrypted message $E=[-241,272,-740,-161,-30,-142]$ decrypted using the key matrix is:

$$\text{D = [104, 105, 32, 32, 32, 32]}$$

The decrypted message $D$ is obtained by converting each integer in the sequence to its corresponding ASCII character. Therefore, the decrypted message is $\text{"hi "}$.

Example Runtime Screenshots

Encryption

Decryption