[LeetCode] 1091. Shortest Path in Binary Matrix

[grandyang]

Given an n x n binary matrix grid, return  the length of the shortest clear path in the matrix. If there is no clear path, return -1.

A clear path in a binary matrix is a path from the top-left cell (i.e., (0, 0)) to the bottom-right cell (i.e., (n - 1, n - 1)) such that:

• All the visited cells of the path are 0.
• All the adjacent cells of the path are 8-directionally connected (i.e., they are different and they share an edge or a corner).

The length of a clear path is the number of visited cells of this path.

Example 1:

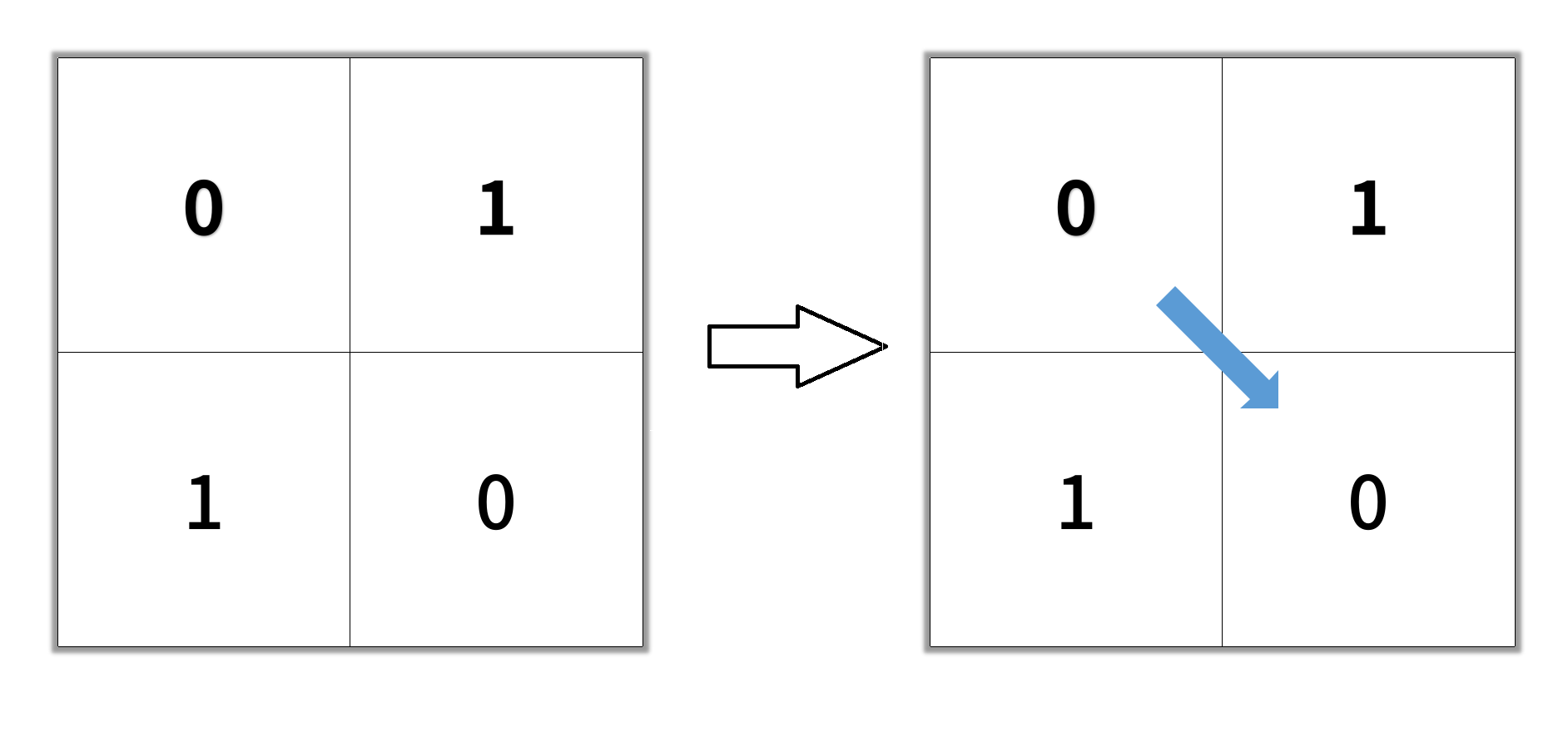
Input: grid = [[0,1],[1,0]]
Output: 2

Example 2:

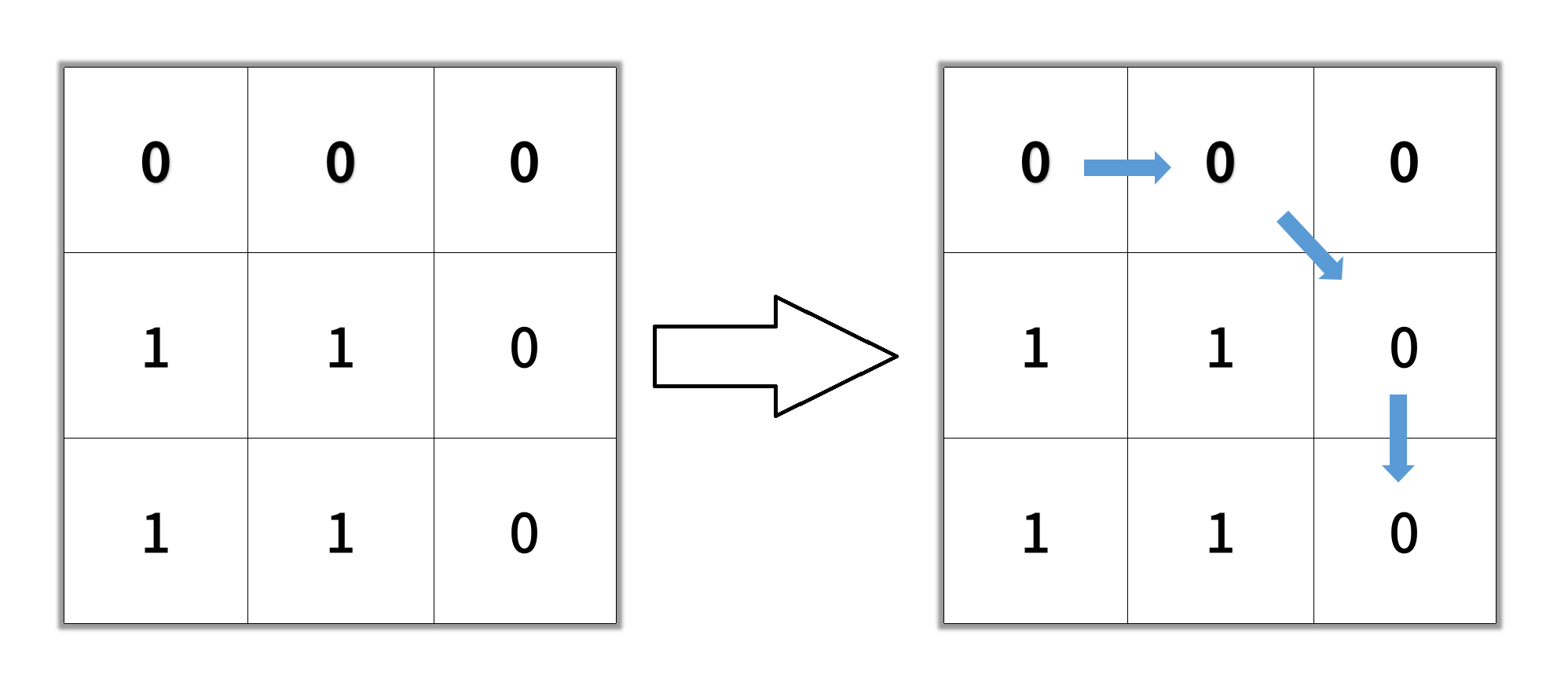
Input: grid = [[0,0,0],[1,1,0],[1,1,0]]
Output: 4

Example 3:

Input: grid = [[1,0,0],[1,1,0],[1,1,0]]
Output: -1

Constraints:

• n == grid.length
• n == grid[i].length
• 1 <= n <= 100
• grid[i][j] is 0 or 1

这道题给了一个 nxn 的二维数组，里面都是0和1，让找出一条从左上角到右下角的干净路径，所谓的干净路径就是均由0组成，并且定义了相邻的位置是八个方向，不仅仅是通常的上下左右。例子中还给了图帮助理解，但是也有一丢丢的误导，博主最开始以为只需要往右，下，和右下三个方向走就行了，其实并不一定，任何方向都是可能的，说白了还是一道迷宫遍历的问题。既然是迷宫遍历求最少步数，那么广度优先遍历 Breadth-First Search 就是不二之选了，还是使用一个队列 queue 来做，初识时将 (0, 0) 放进去，再用一个 TreeSet 来标记访问过的位置。注意这里的方向数组要用到八个方向，while 循环中用的还是经典的层序遍历的写法，就是经典的写法，没有啥特殊的地方，博主感觉已经写了无数次了，在进行这一切之前，先判断一下起始点，若为1，直接返回 -1 即可，参见代码如下：

class Solution {
public:
    int shortestPathBinaryMatrix(vector<vector<int>>& grid) {
        if (grid[0][0] == 1) return -1;
        int res = 0, n = grid.size();
        set<vector<int>> visited;
        visited.insert({0, 0});
        queue<vector<int>> q;
        q.push({0, 0});
        vector<vector<int>> dirs{{-1, 0}, {-1, 1}, {0, 1}, {1, 1}, {1, 0}, {1, -1}, {0, -1}, {-1, -1}};
        while (!q.empty()) {
            ++res;
            for (int i = q.size(); i > 0; --i) {
                auto t = q.front(); q.pop();
                if (t[0] == n - 1 && t[1] == n - 1) return res;
                for (auto dir : dirs) {
                    int x = t[0] + dir[0], y = t[1] + dir[1];
                    if (x < 0 || x >= n || y < 0 || y >= n || grid[x][y] == 1 || visited.count({x, y})) continue;
                    visited.insert({x, y});
                    q.push({x, y});
                }
            }
        }
        return -1;
    }
};

讨论：其实上面的写法基本上属于压线过的 OJ，因为 BFS 基本上属于遍历了所有情况的，当数组中有大量的0的时候，这种方法就显得不是很高效了。论坛上的高分解法，参见大神 lxnn 的帖子，使用到了 A* 搜索，是一种启发式搜索，有兴趣的童鞋可以去研究一下。不过在面试中，一般来说不会考这么难的，基本的 BFS 解法是一定要掌握的。

Github 同步地址:

#1091

参考资料：

https://leetcode.com/problems/shortest-path-in-binary-matrix/

https://leetcode.com/problems/shortest-path-in-binary-matrix/discuss/312706/JAVA-BFS

https://leetcode.com/problems/shortest-path-in-binary-matrix/discuss/313347/A*-search-in-Python

LeetCode All in One 题目讲解汇总(持续更新中...)