[LeetCode] 1145. Binary Tree Coloring Game

[grandyang]

Two players play a turn based game on a binary tree.  We are given the root of this binary tree, and the number of nodes n in the tree.  n is odd, and each node has a distinct value from 1 to n.

Initially, the first player names a value x with 1 <= x <= n, and the second player names a value y with 1 <= y <= n and y != x.  The first player colors the node with value x red, and the second player colors the node with value y blue.

Then, the players take turns starting with the first player.  In each turn, that player chooses a node of their color (red if player 1, blue if player 2) and colors an uncolored neighbor of the chosen node (either the left child, right child, or parent of the chosen node.)

If (and only if) a player cannot choose such a node in this way, they must pass their turn.  If both players pass their turn, the game ends, and the winner is the player that colored more nodes.

You are the second player.  If it is possible to choose such a y to ensure you win the game, return true.  If it is not possible, return false.

Example 1:

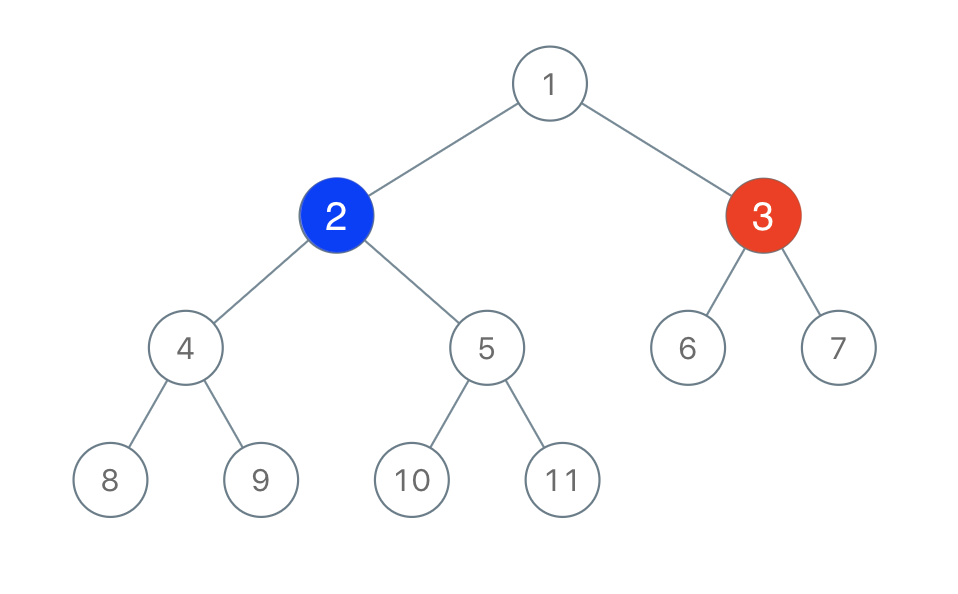
Input: root = [1,2,3,4,5,6,7,8,9,10,11], n = 11, x = 3
Output: true
Explanation: The second player can choose the node with value 2.

Constraints:

• root is the root of a binary tree with n nodes and distinct node values from 1 to n.
• n is odd.
• 1 <= x <= n <= 100

这道题说是两个选手轮流玩一个给二叉树结点上色的游戏，这个二叉树有n个结点，结点值标号也是从1到n，没有重复。说是每个选手轮流给一个结点上色，选手一上红色，选手二上蓝色，之后每个选手只能选择其已经上过色的结点的相连的未上色结点进行上色（即左右子结点和父结点），直到最后两个选手都没法再上色时游戏结束，并且上色的结点多的那个选手获胜。现在假设我们是选手二，而且选手一已经给某个结点x上色了，问我们是否可以赢得这个游戏。题意不是特别好理解，博主读了好几遍总算是弄懂了。那么当选手一选取了某个结点x时，选手二应该选哪些点才能有最大的获胜希望呢，答案是结点x的左右子结点或者父结点，选了左右子结点，则左右子树完全就是选手二的势力范围，选手一无法染指，同理，若是选了父结点，则结点x的兄弟子树就全是选手一的了，所以说对于题目中的例子，选手二的最优解是将结点1上色，这样能上色的结点最多，不过给结点2上色也能赢，问题不大。所以这里，我们只需要统计出三个子树的结点个数，分别是结点x的左右子树，和兄弟子树，只要任意一个子树的结点个数大于所有结点个数的一半，则选手二肯定能赢。所以这道题变成了统计二叉树结点个数，使用递归来做，在递归函数中，首先判断当前结点是否为空，是的话返回0，否则分别对左右子树调用递归，得到左右子树的总结点值。若当前的结点正是选手一选择的起始点，则前面得到的左右子树结点个数就要保存下来，递归函数的返回值是左右子树结点个数加1。回到主函数中，此时已经知道了左右子树的结点个数分别为 left 和 right，则兄弟子树结点个数为总个数减去 left 和 right，再减去1。只要这三个值中的最大的那个大于 n/2，则选手二能赢，参见代码如下：

class Solution {
public:
    bool btreeGameWinningMove(TreeNode* root, int n, int x) {
        int left = 0, right = 0;
        helper(root, x, left, right);
        return max(max(left, right), n - left - right - 1) > n / 2;
    }
    int helper(TreeNode* node, int x, int& left, int& right) {
        if (!node) return 0;
        int l = helper(node->left, x, left, right), r = helper(node->right, x, left, right);
        if (node->val == x) {
            left = l; right = r;
        }
        return l + r + 1;
    }
};

Github 同步地址:

#1145

参考资料：

https://leetcode.com/problems/binary-tree-coloring-game/

https://leetcode.com/problems/binary-tree-coloring-game/discuss/350738/Easy-to-understand-for-everyone

https://leetcode.com/problems/binary-tree-coloring-game/discuss/350570/JavaC%2B%2BPython-Simple-recursion-and-Follow-Up

LeetCode All in One 题目讲解汇总(持续更新中...)