[LeetCode] 1222. Queens That Can Attack the King

[grandyang]

On an 8x8 chessboard, there can be multiple Black Queens and one White King.

Given an array of integer coordinates queens that represents the positions of the Black Queens, and a pair of coordinates king that represent the position of the White King, return the coordinates of all the queens (in any order) that can attack the King.

Example 1:

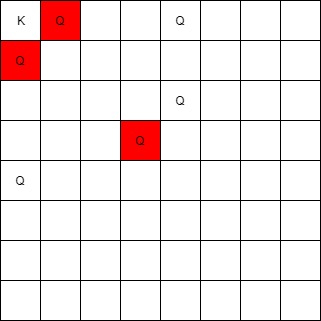
Input: queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0]
Output: [[0,1],[1,0],[3,3]]
Explanation: 
The queen at [0,1] can attack the king cause they're in the same row.
The queen at [1,0] can attack the king cause they're in the same column.
The queen at [3,3] can attack the king cause they're in the same diagnal.
The queen at [0,4] can't attack the king cause it's blocked by the queen at [0,1].
The queen at [4,0] can't attack the king cause it's blocked by the queen at [1,0].
The queen at [2,4] can't attack the king cause it's not in the same row/column/diagnal as the king.

Example 2:

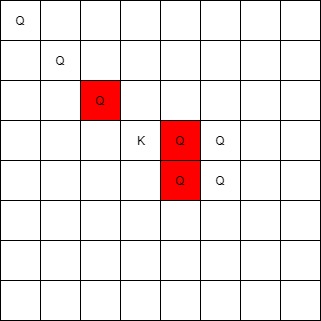
Input: queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3]
Output: [[2,2],[3,4],[4,4]]

Example 3:

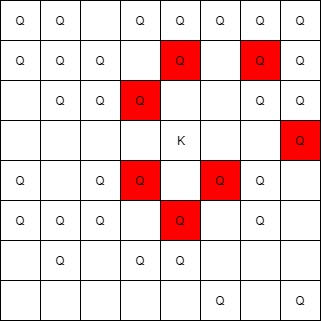
Input: queens = [[5,6],[7,7],[2,1],[0,7],[1,6],[5,1],[3,7],[0,3],[4,0],[1,2],[6,3],[5,0],[0,4],[2,2],[1,1],[6,4],[5,4],[0,0],[2,6],[4,5],[5,2],[1,4],[7,5],[2,3],[0,5],[4,2],[1,0],[2,7],[0,1],[4,6],[6,1],[0,6],[4,3],[1,7]], king = [3,4]
Output: [[2,3],[1,4],[1,6],[3,7],[4,3],[5,4],[4,5]]

Constraints:

• 1 <= queens.length <= 63
• queens[i].length == 2
• 0 <= queens[i][j] < 8
• king.length == 2
• 0 <= king[0], king[1] < 8
• At most one piece is allowed in a cell.

这道题说是在一个 8 by 8 大小的国际象棋的棋盘上，放了多个黑色皇后和一个白色的国王，国际象棋的中的皇后就相当于中国象棋中的车，不过比车更叼，不但能横竖走，还能斜着走，国王就相当于将和帅，现在问有多少个皇后能攻击到国王。题目中的每个例子都十分贴心的配了图，可以更好的帮助我们理解。博主最开始没看清楚题目，认为直接判断每个皇后是否跟国王共线就可以了，但是即便是共线，也不代表皇后就可以攻击到国王，若中间还有其他皇后就不行，就像例子1中的那样。所以视角就应该转移到国王本身，对于棋盘上任意一个非边缘位置，共有八个方向可以去，而每个方向都可能遇到皇后，一旦遇到皇后了，这个方向就不会再遇到其他的皇后了。所以就应该以国王为起点，分别朝八个方向前进，看是否可以遇到皇后。

博主之前写出的解法有点复杂，是分别遍历八个方向的情况，但实际上可以写的更加简洁一些，利用方向变量的 offset，就像在迷宫遍历时，写出四个方向的变量一样，这里八个方向其实就是 [-1, 0, 1] 中任取两个数字分别加上当前的横纵坐标，注意要去掉 (0, 0) 这种情况，因为并不会发生位置的变化。所以当拿到一组偏移量时，就可以进行 while 循环，条件时不越界，当新位置上有皇后时，将该位置加入结果 res，并 break 掉循环，否则再次加上偏移量继续循环。如何快速的知道某个位置上是否有皇后呢，当然不能每次遍历一次所有皇后的位置，太不高效，这里可以建立另一个 8 by 8 大小的二维数组 seen，当 seen[i][j] 为1时，就表示 (i, j) 位置是皇后，参见代码如下：

class Solution {
public:
    vector<vector<int>> queensAttacktheKing(vector<vector<int>>& queens, vector<int>& king) {
        vector<vector<int>> res, seen(8, vector<int>(8));
        for (auto queen : queens) {
            seen[queen[0]][queen[1]] = 1;
        }
        for (int i = -1; i <= 1; ++i) {
            for (int j = -1; j <= 1; ++j) {
                if (i == 0 && j == 0) continue;
                int x = king[0] + i, y = king[1] + j;
                while (min(x, y) >= 0 && max(x, y) < 8) {
                    if (seen[x][y] == 1) {
                        res.push_back({x, y});
                        break;
                    }
                    x += i, y += j;
                }
            }
        }
        return res;
    }
};

Github 同步地址:

#1222

参考资料：

https://leetcode.com/problems/queens-that-can-attack-the-king/

https://leetcode.com/problems/queens-that-can-attack-the-king/discuss/403755/C%2B%2B-Tracing

https://leetcode.com/problems/queens-that-can-attack-the-king/discuss/403687/Java-short-and-concise-beat-100

LeetCode All in One 题目讲解汇总(持续更新中...)