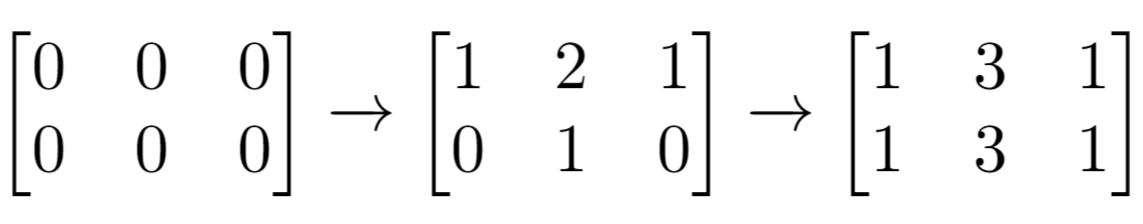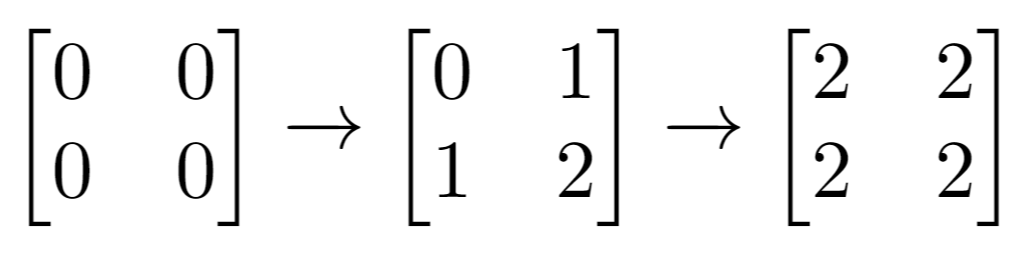-
-
Notifications
You must be signed in to change notification settings - Fork 739
Description
There is an m x n matrix that is initialized to all 0's. There is also a 2D array indices where each indices[i] = [ri, ci] represents a 0-indexed location to perform some increment operations on the matrix.
For each location indices[i], do both of the following:
- Increment all the cells on row
ri. - Increment all the cells on column
ci.
Given m, n, and indices, return *the number of odd-valued cells in the matrix after applying the increment to all locations in *indices.
Example 1:
Input: m = 2, n = 3, indices = [[0,1],[1,1]]
Output: 6
Explanation: Initial matrix = [[0,0,0],[0,0,0]].
After applying first increment it becomes [[1,2,1],[0,1,0]].
The final matrix is [[1,3,1],[1,3,1]], which contains 6 odd numbers.
Example 2:
Input: m = 2, n = 2, indices = [[1,1],[0,0]]
Output: 0
Explanation: Final matrix = [[2,2],[2,2]]. There are no odd numbers in the final matrix.
Constraints:
1 <= m, n <= 501 <= indices.length <= 1000 <= ri < m0 <= ci < n
Follow up: Could you solve this in O(n + m + indices.length) time with only O(n + m) extra space?
这道题给了一个大小为 m by n 的矩阵,初始化均为0,又给了一个坐标数组 indices,说是对于其中的每个坐标 (r, c),将对应的行和列上的数字分别自增1,最后问数组中有多少个数字是奇数。当然最简单暴力的解法就是就是遍历每个坐标,分别将对应的行列上的数字自增1,然后最后再判断奇偶,虽然这是一道 Easy 的题目,但博主还是怀疑这种方法可能会超时,所以根本就没有尝试。对于每个坐标都遍历一次行和列,实在是不太高效,因为该行和该列可能后面还会多次出现,有没有办法能够一次性统计出某行某列到底需要更新多少次呢?答案是肯定的,这里可以建立两个数组 rowCnt 和 colCnt,分别来统计某行和某列需要更新的次数。之后遍历整个初始数组,对于任意位置 (i, j),去 rowCnt 和 colCnt 中取出行i和列j需要的更新次数,二者之和就是当前位置需要增加的数字,直接判断奇偶,奇数的话加到结果 res 中即可,参见代码如下:
class Solution {
public:
int oddCells(int m, int n, vector<vector<int>>& indices) {
int res = 0;
vector<int> rowCnt(m), colCnt(n);
for (auto idx : indices) {
++rowCnt[idx[0]];
++colCnt[idx[1]];
}
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
res += (rowCnt[i] + colCnt[j]) % 2;
}
}
return res;
}
};
Github 同步地址:
参考资料:
https://leetcode.com/problems/cells-with-odd-values-in-a-matrix/
LeetCode All in One 题目讲解汇总(持续更新中...)
喜欢请点赞,疼爱请打赏❤️~.~
微信打赏
Venmo 打赏