[LeetCode] 490. The Maze

[grandyang]

 

There is a ball in a maze with empty spaces and walls. The ball can go through empty spaces by rolling up, down, left or right, but it won't stop rolling until hitting a wall. When the ball stops, it could choose the next direction.

Given the ball's start position, the destination and the maze, determine whether the ball could stop at the destination.

The maze is represented by a binary 2D array. 1 means the wall and 0 means the empty space. You may assume that the borders of the maze are all walls. The start and destination coordinates are represented by row and column indexes.

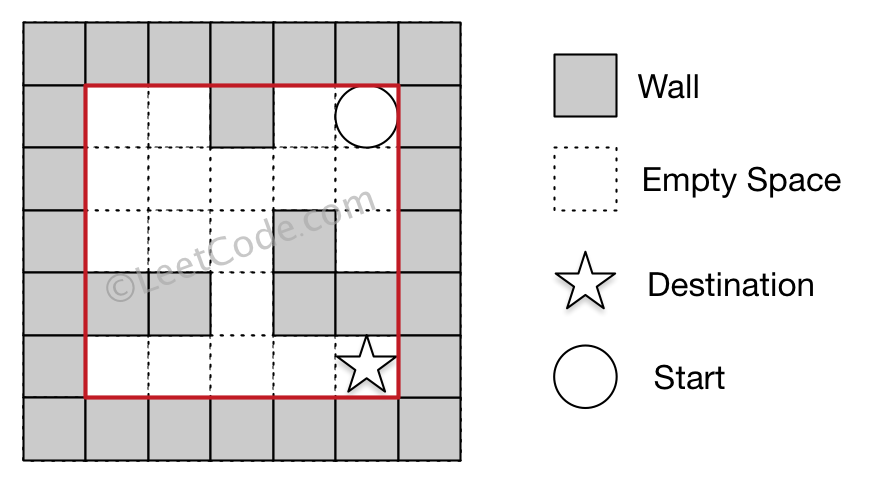
Example 1

Input 1: a maze represented by a 2D array

0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0

Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (4, 4)

Output: true
Explanation: One possible way is : left -> down -> left -> down -> right -> down -> right.

 

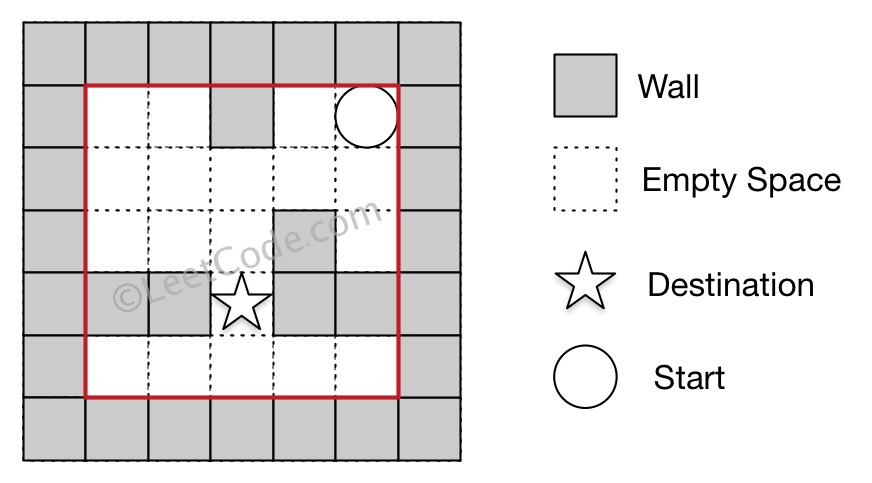
Example 2

Input 1: a maze represented by a 2D array

0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0

Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (3, 2)

Output: false
Explanation: There is no way for the ball to stop at the destination.

 

Note:

1. There is only one ball and one destination in the maze.
2. Both the ball and the destination exist on an empty space, and they will not be at the same position initially.
3. The given maze does not contain border (like the red rectangle in the example pictures), but you could assume the border of the maze are all walls.
4. The maze contains at least 2 empty spaces, and both the width and height of the maze won't exceed 100.

 

这道题让我们遍历迷宫，但是与以往不同的是，这次迷宫是有一个滚动的小球，这样就不是每次只走一步了，而是朝某一个方向一直滚，直到遇到墙或者边缘才停下来，博主记得貌似之前在手机上玩过类似的游戏。那么其实还是要用 DFS 或者 BFS 来解，只不过需要做一些修改。先来看 DFS 的解法，用 DFS 的同时最好能用上优化，即记录中间的结果，这样可以避免重复运算，提高效率。这里用二维记忆数组 memo 来保存中间结果，然后用 maze 数组本身通过将0改为 -1 来记录某个点是否被访问过，这道题的难点是在于处理一直滚的情况，其实也不难，有了方向，只要一直在那个方向上往前走，每次判读是否越界了或者是否遇到墙了即可，然后对于新位置继续调用递归函数，参见代码如下：

  

解法一：

class Solution {
public:
    vector<vector<int>> dirs{{0,-1},{-1,0},{0,1},{1,0}};
    bool hasPath(vector<vector<int>>& maze, vector<int>& start, vector<int>& destination) {int m = maze.size(), n = maze[0].size();
        return helper(maze, start[0], start[1], destination[0], destination[1]);
    }
    bool helper(vector<vector<int>>& maze, int i, int j, int di, int dj) {
        if (i == di && j == dj) return true;
        bool res = false;
        int m = maze.size(), n = maze[0].size();
        maze[i][j] = -1;
        for (auto dir : dirs) {
            int x = i, y = j;
            while (x >= 0 && x < m && y >= 0 && y < n && maze[x][y] != 1) {
                x += dir[0]; y += dir[1];
            }
            x -= dir[0]; y -= dir[1];
            if (maze[x][y] != -1) {
                res |= helper(maze, x, y, di, dj);
            }
        }
        return res;
    }
};

 

同样的道理，对于 BFS 的实现需要用到队列 queue，在对于一直滚的处理跟上面相同，参见代码如下：

 

解法二：

class Solution {
public:
    bool hasPath(vector<vector<int>>& maze, vector<int>& start, vector<int>& destination) {
        if (maze.empty() || maze[0].empty()) return true;
        int m = maze.size(), n = maze[0].size();
        vector<vector<bool>> visited(m, vector<bool>(n, false));
        vector<vector<int>> dirs{{0,-1},{-1,0},{0,1},{1,0}};
        queue<pair<int, int>> q;
        q.push({start[0], start[1]});
        visited[start[0]][start[1]] = true;
        while (!q.empty()) {
            auto t = q.front(); q.pop();
            if (t.first == destination[0] && t.second == destination[1]) return true;
            for (auto dir : dirs) {
                int x = t.first, y = t.second;
                while (x >= 0 && x < m && y >= 0 && y < n && maze[x][y] == 0) {
                    x += dir[0]; y += dir[1];
                }
                x -= dir[0]; y -= dir[1];
                if (!visited[x][y]) {
                    visited[x][y] = true;
                    q.push({x, y});
                }
            }
        }
        return false;
    }
};

 

Github 同步地址：

#490

 

类似题目：

The Maze II

The Maze III

 

参考资料：

https://leetcode.com/problems/the-maze/

https://leetcode.com/problems/the-maze/discuss/97081/java-bfs-solution

https://leetcode.com/problems/the-maze/discuss/97112/Short-Java-DFS-13ms-Solution

https://leetcode.com/problems/the-maze/discuss/97089/java-dfs-solution-could-anyone-tell-me-how-to-calculate-the-time-complexity

 

LeetCode All in One 题目讲解汇总(持续更新中...) 

[crazy-shawn-liu]

[[0,0,1,0,0],
[0,0,0,0,0],
[0,0,0,1,0],
[1,1,0,1,1],
[0,0,0,0,0]]
[0,4]
[1,2]
这个case小球是停不下来的，因为到[1,2]以后，左侧和下侧都没有墙壁，为什么答案给出的是true，求指导。。
多谢大神。

[grandyang]

[[0,0,1,0,0],
[0,0,0,0,0],
[0,0,0,1,0],
[1,1,0,1,1],
[0,0,0,0,0]]
[0,4]
[1,2]
这个case小球是停不下来的，因为到[1,2]以后，左侧和下侧都没有墙壁，为什么答案给出的是true，求指导。。
多谢大神。

不用停下来，一直滚到 [1, 0]，然后向下滚到 [2, 0]，向右滚到[2, 2]，再向下就行了。

[crazy-shawn-liu]

明白了，多谢：）