[LeetCode] 883. Projection Area of 3D Shapes

[grandyang]

On a N * N grid, we place some 1 * 1 * 1 cubes that are axis-aligned with the x, y, and z axes.

Each value v = grid[i][j] represents a tower of v cubes placed on top of grid cell (i, j).

Now we view the  projection  of these cubes onto the xy, yz, and zx planes.

A projection is like a shadow, that maps our 3 dimensional figure to a 2 dimensional plane.

Here, we are viewing the "shadow" when looking at the cubes from the top, the front, and the side.

Return the total area of all three projections.

Example 1:

Input: [[2]]
Output: 5

Example 2:

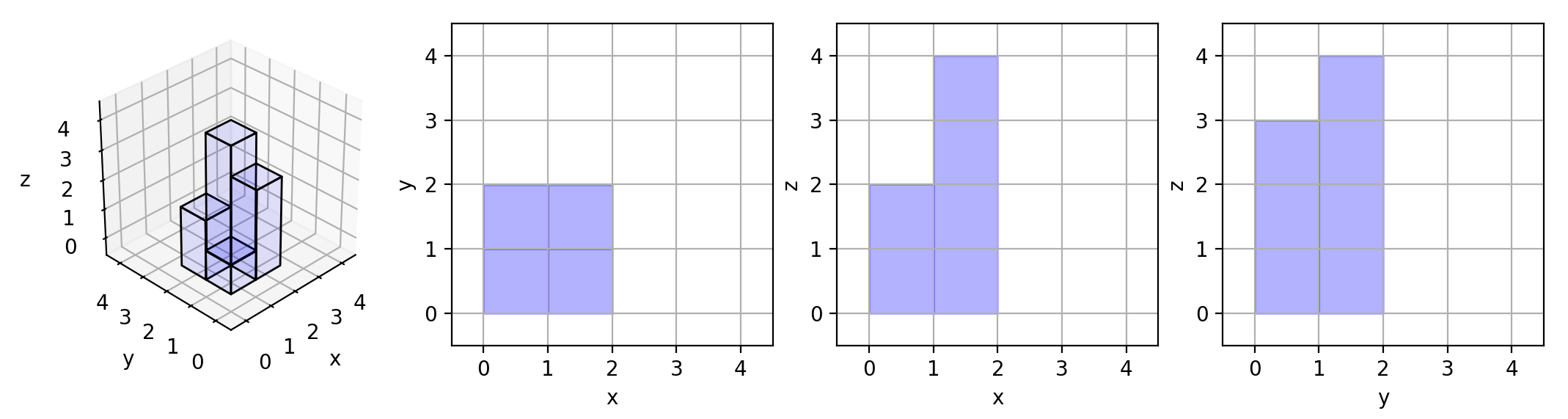
Input: [[1,2],[3,4]]
Output: 17
Explanation:
Here are the three projections ("shadows") of the shape made with each axis-aligned plane.

Example 3:

Input: [[1,0],[0,2]]
Output: 8

Example 4:

Input: [[1,1,1],[1,0,1],[1,1,1]]
Output: 14

Example 5:

Input: [[2,2,2],[2,1,2],[2,2,2]]
Output: 21

Note:

• 1 <= grid.length = grid[0].length <= 50
• 0 <= grid[i][j] <= 50

这道题给了我们一个二维数组 grid，用来表示一个 3D 物体形状，表示方法是 grid[i][j] 表示在 (i, j) 位置上的高度，就像垒积木一样，累出了一个三维物体。然后让我们计算三个方向的投影面积之和，所谓的三个方向分别是上方 Top，前方 Front，和侧方 Side。用过一些三维建模软件（例如 Maya， 3DMax）的同学，对这个应该不陌生。我们先来考虑正上方投影面积如何计算，由于题目中说了 grid 数组的宽和高相等，那么上方投影就是一个正方形，前提是每个 grid[i][j] 的值都大于0的话。因为若 grid 数组中有0存在，则表示正方形投影会缺少了一块。由于这个大的正方形投影是由 nxn 个小的正方形组成，那么实际上我们只要统计出小正方形的个数，那么大正方形投影的面积也就知道了（是不有点微积分的感觉）。所以我们在遍历的过程中，只要判断若 grid[i][j] 大于0，则结果 res 自增1即可。下面再来考虑另外两个方向的投影怎么计算，另两个方向的投影的可能是不规则图形，参见题目中给的那个图，如果仔细观察的话，其投影图像的每个阶段的高其实就是各行或各列中的最大值，这也不难理解，就像城市中耸立的高度不同的大楼，若要描出城市的轮廓，那么描出来的肯定都是每个位置上最高建筑物的轮廓。那么问题就变成了累加各行各列的最大值。我们实际上在一次遍历中就能完成，使用了一个小 trick，那就是在第二层 for 循环中，行最大值 rowMax 就是不断用 grid[i][j] 来更新，而列最大值 colMax 就是不断用 grid[j][i] 来更新，巧妙的交换i和j，实现了目标。然后分别把更新出来的行列最大值加到结果 res 中即可，参见代码如下：

class Solution {
public:
    int projectionArea(vector<vector<int>>& grid) {
		int n = grid[0].size(), res = 0;
		for (int i = 0; i < n; ++i) {
			int rowMax = 0, colMax = 0;
			for (int j = 0; j < n; ++j) {
                if (grid[i][j] > 0) ++res;
				rowMax = max(rowMax, grid[i][j]);
				colMax = max(colMax, grid[j][i]);
			}
			res += rowMax + colMax;
		}
		return res;
    }
};

Github 同步地址:

#883

参考资料：

https://leetcode.com/problems/projection-area-of-3d-shapes/

https://leetcode.com/problems/projection-area-of-3d-shapes/discuss/156726/C%2B%2BJavaPython-Straight-Forward

https://leetcode.com/problems/projection-area-of-3d-shapes/discuss/156771/11-line-1-pass-Java-code-and-explanation-of-the-problem-time-O(N-2)-space-O(1).

LeetCode All in One 题目讲解汇总(持续更新中...)