[LeetCode] 885. Spiral Matrix III

[grandyang]

On a 2 dimensional grid with R rows and C columns, we start at (r0, c0) facing east.

Here, the north-west corner of the grid is at the first row and column, and the south-east corner of the grid is at the last row and column.

Now, we walk in a clockwise spiral shape to visit every position in this grid.

Whenever we would move outside the boundary of the grid, we continue our walk outside the grid (but may return to the grid boundary later.)

Eventually, we reach all R * C spaces of the grid.

Return a list of coordinates representing the positions of the grid in the order they were visited.

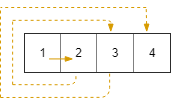
Example 1:

Input: R = 1, C = 4, r0 = 0, c0 = 0
Output: [[0,0],[0,1],[0,2],[0,3]]

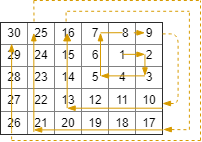
Example 2:

Input: R = 5, C = 6, r0 = 1, c0 = 4
Output: [[1,4],[1,5],[2,5],[2,4],[2,3],[1,3],[0,3],[0,4],[0,5],[3,5],[3,4],[3,3],[3,2],[2,2],[1,2],[0,2],[4,5],[4,4],[4,3],[4,2],[4,1],[3,1],[2,1],[1,1],[0,1],[4,0],[3,0],[2,0],[1,0],[0,0]]

Note:

1. 1 <= R <= 100
2. 1 <= C <= 100
3. 0 <= r0 < R
4. 0 <= c0 < C

这道题给了我们一个二维矩阵，还给了其中一个位置，让从这个位置开始搓一个螺旋丸，哦不，是螺旋打印矩阵。具体怎么螺旋打印呢，题目中给了例子，又给了示例图，真的是很贴心呢。可以看出来，首先是打印给定的位置，然后向右走一位，打印出来，再向下方走一位打印，再向左边走两位打印，再向上方走三位打印，以此类推，螺旋打印。那仔细观察，可以发现，刚开始只是走一步，后来步子越来越大，若只看每个方向走的距离，可以得到如下数组 1,1,2,2,3,3... 步长有了，下面就是方向了，由于确定了起始是向右走，那么方向就是 右->下->左->上 这样的循环。方向和步长都分析清楚了，现在就可以尝试进行遍历了。由于最终是会遍历完所有的位置的，那么最后结果 res 里面的位置个数一定是等于 RxC 的，所以循环的条件就是当结果 res 中的位置数小于 R*C。我们还需要一个变量 step 表示当前的步长，初始化为1。在循环中，首先要想右走 step 步，一步一步走，走到一个新的位置上，要进行判断，若当前位置没有越界，才能加入结果 res 中，由于每次都要判断，所以把这部分抽取出来，放到一个子函数中。由于是向右走，每走一步之后，c0 都要自增1。右边走完了之后，再向下方走 step 步，同理，每走一步之后，要将 r0 自增1。再向左边走之前，要将步数增1，不然无法形成正确的螺旋，同理，再完成向上方走 step 步之后，step 要再增1，参见代码如下：
解法一：

class Solution {
public:
    vector<vector<int>> spiralMatrixIII(int R, int C, int r0, int c0) {
        vector<vector<int>> res;
        int step = 1;
        while (res.size() < R * C) {
        	for (int i = 0; i < step; ++i) add(R, C, r0, c0++, res);
        	for (int i = 0; i < step; ++i) add(R, C, r0++, c0, res);
        	++step;
        	for (int i = 0; i < step; ++i) add(R, C, r0, c0--, res);
        	for (int i = 0; i < step; ++i) add(R, C, r0--, c0, res);
        	++step;
        }
        return res;
    }
    void add(int R, int C, int x, int y, vector<vector<int>>& res) {
    	if (x >= 0 && x < R && y >= 0 && y < C) res.push_back({x, y});
    }
};

上面的方法 for 循环太多，看的很木乱，可以用两个数组 dirX 和 dirY 来控制下一个方向，就像迷宫遍历中的那样，这样只需要一个变量 cur，来分别到 dirX 和 dirY 中取值，初始化为0，表示向右的方向。从螺旋遍历的机制可以看出，每当向右或者向左前进时，步长就要加1，那么我们只要判断当 cur 为0或者2的时候，step 就自增1。由于 cur 初始化为0，所以刚开始 step 就会增1，那么就可以将 step 初始化为0，同时还需要把起始位置提前加入结果 res 中。此时在 while 循环中只需要一个 for 循环即可，朝当前的 cur 方向前进 step 步，r0 加上 dirX[cur]，c0 加上 dirY[cur]，若没有越界，则加入结果 res 中即可。之后记得 cur 要自增1，为了防止越界，对4取余，就像循环数组一样的操作，参见代码如下：
解法二：

class Solution {
public:
    vector<vector<int>> spiralMatrixIII(int R, int C, int r0, int c0) {
        vector<vector<int>> res{{r0, c0}};
        vector<int> dirX{0, 1, 0, -1}, dirY{1, 0, -1, 0};
        int step = 0, cur = 0;
        while (res.size() < R * C) {
        	if (cur == 0 || cur == 2) ++step;
        	for (int i = 0; i < step; ++i) {
        		r0 += dirX[cur]; c0 += dirY[cur];
        		if (r0 >= 0 && r0 < R && c0 >= 0 && c0 < C) res.push_back({r0, c0});
        	}
        	cur = (cur + 1) % 4;
        }
        return res;
    }
};

我们也可以不使用方向数组，若仔细观察 右->下->左->上 四个方向对应的值 (0, 1) -> (1, 0) -> (0, -1) -> (-1, 0), 实际上，下一个位置的x值是当前的y值，下一个位置的y值是当前的-x值，因为两个方向是相邻的两个方向是垂直的，由向量的叉乘得到 (x, y, 0) × (0, 0, 1) = (y, -x, 0)。所以可以通过当前的x和y值，来计算出下一个位置的值。同理，根据之前的说的步长数组 1,1,2,2,3,3...，可以推出通项公式为 n/2 + 1，这样连步长变量 step 都省了，不过需要统计当前已经遍历的位置的个数，实在想偷懒，也可以用 res.size() 来代替，参见代码如下：
解法三：

class Solution {
public:
    vector<vector<int>> spiralMatrixIII(int R, int C, int r0, int c0) {
        vector<vector<int>> res{{r0, c0}};
        int x = 0, y = 1, t = 0;
        for (int k = 0; res.size() < R * C; ++k) {
        	for (int i = 0; i < k / 2 + 1; ++i) {
        		r0 += x; c0 += y;
        		if (r0 >= 0 && r0 < R && c0 >= 0 && c0 < C) res.push_back({r0, c0});
        	}
        	t = x; x = y; y = -t;
        }
        return res;
    }
};

Github 同步地址:

#885

类似题目：

Spiral Matrix II

Spiral Matrix

参考资料：

https://leetcode.com/problems/spiral-matrix-iii/

https://leetcode.com/problems/spiral-matrix-iii/discuss/158970/C%2B%2BJavaPython-112233-Steps

https://leetcode.com/problems/spiral-matrix-iii/discuss/163370/Simple-East-to-Understand-Java-solution

https://leetcode.com/problems/spiral-matrix-iii/discuss/158977/Java-15-lines-concise-solution-with-comments

LeetCode All in One 题目讲解汇总(持续更新中...)