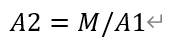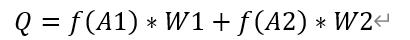GitHub是全球最大的基于Git的代码托管平台之一,许多开发者使用GitHub来管理和协作开源项目。GitHub不仅仅是一个代码托管平台,还提供了许多工具和功能,如问题跟踪、代码审核、协作工具等,这些功能使得开发者可以更好地管理和协作项目。 开发者团队协作能力展现出开发者参与团队项目的积极程度,能够筛选出GitHub社区中比较活跃的开发者,同时也反应出了开发者与协作者完成任务的能力,那么如何去统计和计算开发者团队协作能力是一个备受关注的话题。 在一个开源社区里,如何衡量以为开发者的团队协作能力?
目标是激励更多的开发者积极参与到开源项目中,共同贡献代码、参与讨论,为项目的发展做出更多的贡献。通过对开发者团队能力协作的评估,可以调动开发的积极性为开源社区建设贡献自己的一份力量。
团队协作能力不仅包括代码的编写,还包括与开发者有过协作的开发者的数量与开发者与其协作者之间紧密程度的平均值。 第一, 与开发者有过协作的开发者的数量,统计GitHub全域与此开发者有关协作的开发者数量可以记作A1 第二, 统计开发者与其协作者之间的紧密程度,如与此开发者有过评论回复或者pr的一次就记为1分,两次就记为2分,以此类推。 第三, 计算开发者与其协作者之间的紧密程度平均值,使用第二步计算出来的紧密程度除以第一步计算出来的人数则可计算出紧密程度的平均值。 通过对着两个指标的计算,能够非常直观的反应出项目开发者的团队协作能力,最后在通过critic权重计算出来两个指标对应的权重,然后进行相应计算最后得出分数,分数越高,表示开发者的团队协作能力越高。
1. 确定指标评判方式
以下是团队协作能力的计算公式:
公式(1):
公式(2):
公式(3):
公式(4):
团队协作能力使用两个指标来进行评判分别是在全域中与开发者协作过的协作者数量在这边记作A1和开发者与其协作者之间的精密成都的平均值记作A2。其中A1在数据中很容易的出来,A2是使用开发者与所有协作者的紧密程度总和(记作M)/协作过的开发者数量(A1)来得出,然而协作者的紧密程度是通过开发者和协作者在某个issue或者pr中进行评论互动,评论互动一次则加一分以此类推,最后算出每一个协作者与开发者之间的紧密程度做总和(记作M)
| 开发者 | 协作者数量 | 紧密程度之和 | 紧密程度的平均值 |
|---|---|---|---|
| Zenlex | 1 | 1 | 1 |
| Rich-iannone | 4 | 18 | 4.5 |
| xsnoopy | 1 | 2 | 2 |
| gxalpha | 8 | 64 | 8 |
| shirblc | 1 | 1 | 1 |
| dreamsparkx | 1 | 1 | 1 |
上面中第一列是开发者的名字,第二列是对应的与开发者有过协作的协作者的数量,第三列是开发者与全域协作者的紧密程度之和,同时第四列是计算出来的紧密程度的平均值(A2=紧密程度之和/协作者的数量)。
接下来,分别给出公式(4)中映射函数f的计算方式和权重W的确定依据,并进行指标模型的合理性分析。
2. 影响因素权重决定
CRITIC权重法是一种基于数据波动性的客观赋权法。其思想在于两项指标,分别是波动性(对比强度)和冲突性(相关性)指标。对比强度使用标准差进行表示,如果数据标准差越大说明波动越大,权重会越高;冲突性使用相关系数进行表示,如果指标之间的相关系数值越大,说明冲突性越小,那么其权重也就越低。权重计算时,对比强度与冲突性指标相乘,并且进行归一化处理,即得到最终的权重。其核心思想是将决策问题转化为对一系列标准的评估,这些标准应该可以定量地描述问题的各个方面。选择最优决策方案的过程就是计算各个备选方案在每个标准下的得分,并根据标准的重要性加权计算总得分,最后选择综合得分最高的。
CRITIC权重法利用了数据的波动性和相关关系情况,并非数字越大就说明越重要,完全利用数据自身的客观属性,便于进行科学评价。在进行CRITIC分析之前,通常需要对数据进行量纲化处理,一般使用正向化或逆向化处理,但不建议使用标准化处理,原因是如果使用标准化处理,标准差全部都变成数字1,即所有指标的标准差完全一致,这就导致波动性指标没有意义。
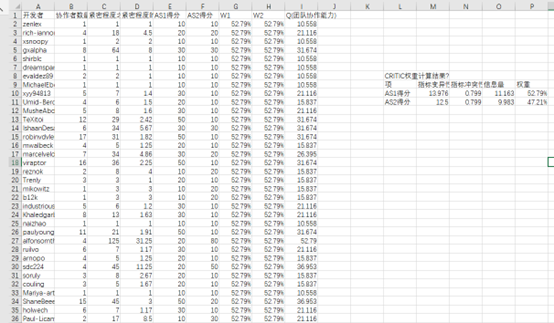
SPSS软件平台提供了广泛的高级统计分析和机器学习算法,以及文本分析等功能,同时也具备开源可扩展性,并且可以轻松与大数据集成,从而实现无缝部署到应用程序中的功能。使用SPSS软件平台,可以更加精确地分析出影响指标的四个因素之间的权重分布,为进一步的研究和应用提供了有力的支持。 SPSSAU共输出一个表格,表格中包括指标变异性,冲突性指标的具体值,并且得到信息量值(指标变异性*指标冲突性),并得到最后的权重(即信息量的归一化值)。如表2所示:
团队协作能力一共两个影响因素分别是协作者的数量和开发者与其协作者之间紧密程度的平均值,通过这两个指标分别计算出AS1和AS2的得分(具体AS1、AS2)公式在后续给出,然后AS1与AS2通过CRITIC权重法确定权重值W1,W2数据展示如下:
| 协作者数量 | 紧密程度之和 | 紧密程度的平均值 | AS1得分 | AS2得分 | W1 | W2 | 团队协作值 |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 20 | 20 | 52.79% | 47.21% | 10 |
| 4 | 18 | 4.5 | 10 | 10 | 52.79% | 47.21% | 30 |
| 1 | 2 | 2 | 30 | 30 | 52.79% | 47.21% | 10 |
| 8 | 64 | 8 | 10 | 10 | 52.79% | 47.21% | 10 |
| 1 | 1 | 1 | 10 | 10 | 52.79% | 47.21% | 10 |
| 1 | 1 | 1 | 10 | 10 | 52.79% | 47.21% | 10 |
3. 区间得分的分析依据
对单个影响因素例如协作数量即为A1,在指标计算模型中它的具体价值与对团队协作能力的贡献值以分段函数的方式确定,下面以影响因素A1为例,给出映射函数 f 的设计依据,并进行合理性分析。这里先给出对应上述两个影响因素的映射函数 f 的表达式如公式所示:
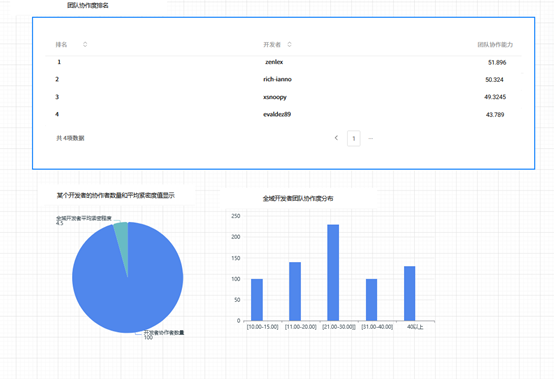
下面以协作者人数A1为例,描述分段函数的设计依据,并进行合理性分析。 一个开发者在github全域中的合作者人数越多,可能反应出这个开发者参与过的项目多,团队协作次数多,同时也有一定可能与其他开发者互动的也多。所以统计一个开发者全域合作者的人数可以反应此开发者的团队协作能力,合作者越多,说明团队协作能力就越强,分数就越高。
1、开源软件项目定性和定量分析指标———chaoss指标解析
https://chaoss.community/kb-metrics-and-metrics-models/
2、文献引用:
基于混合神经网络的开源社区软件开发者人力资源价值预测_汤佳杰