A time delay estimation method for event-based time-series.
This repository contains the source code, demonstration data, unit tests, benchmarks as well as research experiments for the Nearest Advocate Algorithm.
- Github-Repository: https://github.com/iot-salzburg/nearest-advocate
- Pip-Package: https://pypi.org/project/nearest-advocate/.
This package focuses on the time delay estimation between two event-based time-series that are relatively shifted by an unknown time offset. An event-based time-series is given by a set of timestamps of certain events. If you want to guarantee synchronous measurements in advance or estimate the time delay of continuous measurements sampled at a constant rate, you might want to use other methods. However, in some use cases, performing an event detection and then estimating the relative time delay has advantages. The Nearest Advocate method provides a precise time delay estimation in event-based time-series that is robust against imprecise timestamps, a high fraction of missing events, and clock drift. Time delay estimation also known as the correction of time offsets and time lags as well as time synchronization.
Install the package with:
pip install nearest_advocateOpen Python and import and use it for time delay estimation of event-based time-series:
import numpy as np
import nearest_advocateCreate a reference array whose inter-event intervals are sampled from a normal distribution. The signal array is a clone of the reference´, shifted by np.pi and added Gaussian noise. The event's timestamps of both arrays must be sorted.
arr_ref = np.sort(np.cumsum(np.random.normal(loc=1, scale=0.25, size=1000)))
arr_sig = np.sort(arr_ref + np.pi + np.random.normal(loc=0, scale=0.1, size=1000))The function nearest_advocate.nearest_advocate returns a two-columned array with all investigated time-shifts and their mean distances, i.e., the measure of the synchronicity between both arrays (lower is better).
time_shifts = nearest_advocate.nearest_advocate(arr_ref=arr_ref, arr_sig=arr_sig, td_min=-60, td_max=60, sps=20)
time_shift, min_mean_dist = time_shifts[np.argmin(time_shifts[:,1])]
print(f"Found an optimum at {time_shift:.4f}s with a minimal mean distance of {min_mean_dist:.6f}s")
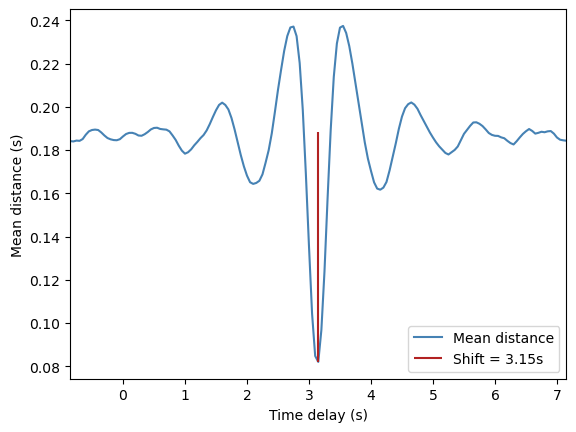
#> Found an optimum at 3.15s with a minimal mean distance of 0.079508sThe time delay estimation is 3.15 seconds which is pretty close to the true one. Create a plot of the resulting characteristic curve of Nearest Advocate, the global minimum of the curve is used as time delay estimation.
import matplotlib.pyplot as plt
plt.plot(time_shifts[:,0], time_shifts[:,1], color="steelblue", label="Mean distance")
plt.vlines(x=time_shift, ymin=min_mean_dist, ymax=np.mean(time_shifts[:,1]), color="firebrick", label=f"Shift = {time_shift:.2f}s")
plt.xlim(time_shift-4, time_shift+4)
plt.xlabel("Time delay (s)")
plt.ylabel("Mean distance (s)")
plt.legend(loc="lower right")
plt.show()To apply the Nearest Advocate algorithm symmetrically, just pass the flag symmetric=True in the method:
time_shifts = nearest_advocate.nearest_advocate(arr_ref=arr_ref, arr_sig=arr_sig, td_min=-60, td_max=60, sps=20, symmetric=True)
time_shift, min_mean_dist = time_shifts[np.argmin(time_shifts[:,1])]
print(f"Found an optimum at {time_shift:.4f}s with a minimal mean distance of {min_mean_dist:.6f}s")
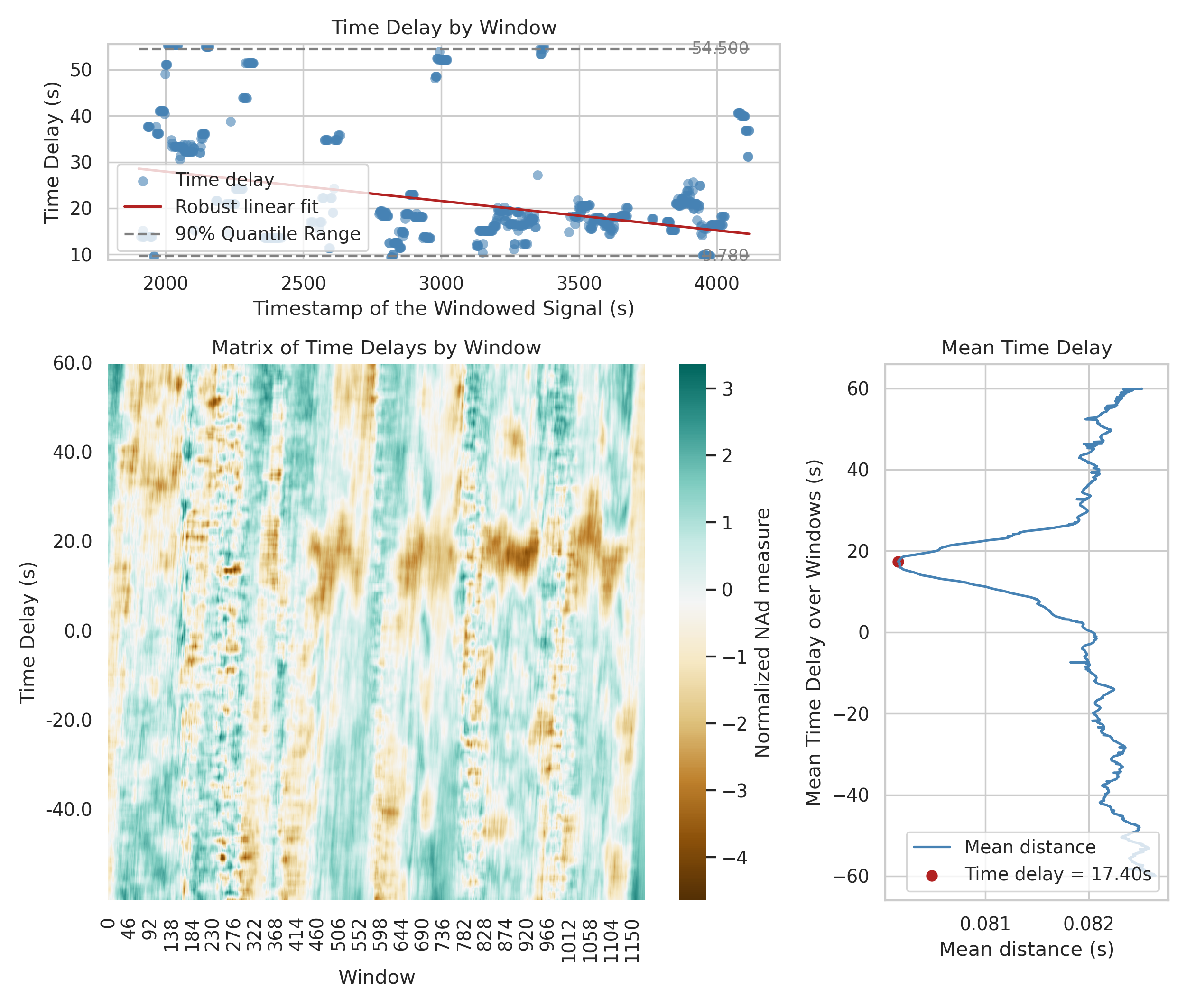
#> Found an optimum at 3.15s with a minimal mean distance of 0.079508sUsing the NAd in sliding windows, it is possible to estimate the linear or non-linear trend of the relatve clock drift between two clocks. To do so, both event time-series should be very long in terms of their number of elements. A Jupyter notebook is provided to adapt this functionality to other applications experiments/application_nonlinear_correction.ipynb.
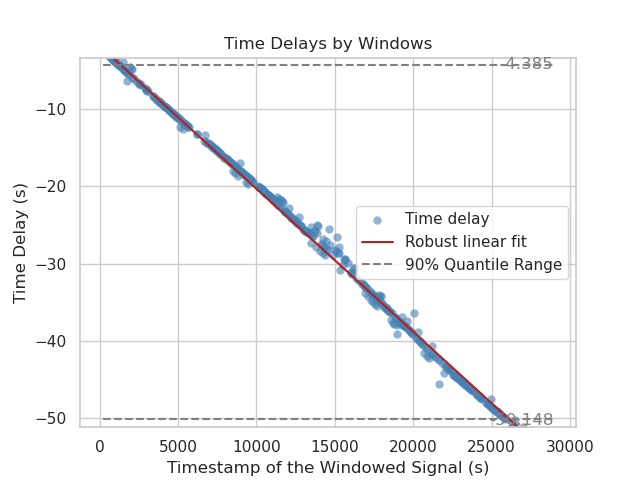
Example of a linear clock-drift correction:
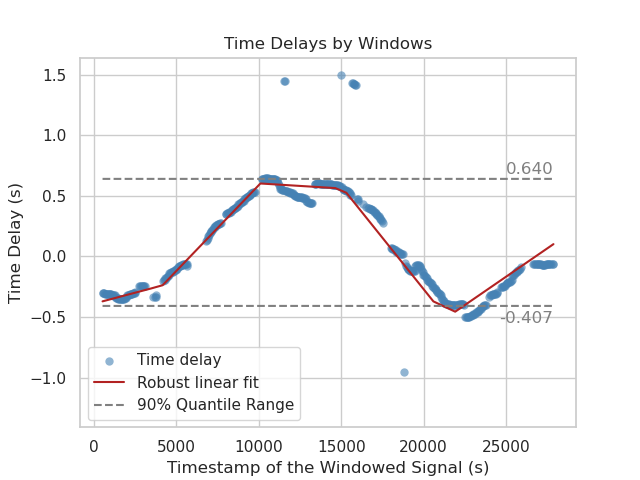
Example of a subsequent nonlinear clock-drift correction:
This algorithm is so robust against data quality issues, that it is even possible to estimate the time-delay between two event-based measurements of different observations. In experiments/application_different_observations.ipynb it is demonstrated how to apply the NAd for breathing and step events from the same participant, that uses the fact that both frequencies are slightly interdependent.
Applied methods for windowed Nearest Advocate, linear and nonlinear clock-drift correction and advanced plotting is provided in experiments/nearest_advocate_windowed with sample Jupyter notebooks of how to use them in the parent directory.
cd /go/to/path
git clone https://github.com/iot-salzburg/nearest-advocate
cd nearest-advocate
pip install -r requirements.txtFor reproducibility, the experiments were run in Python 3.9 inside a container environment using the Docker orchestration software with the image cschranz/gpu-jupyter and tag v1.4\_cuda-11.0\_ubuntu-20.04, available on Dockerhub.
Build the Cython-version of the algorithm with:
cd src
python setup.py build_ext --inplaceCurrently, the Cython-version is under development and will be available soon.
Run the test scripts:
python tests/test_algorithm.py
#> Testing numba-version: ok
#> Testing Cython-version: ok
#> Testing Python-version: ok
python tests/test_performances.py
#> ################# Test and compare shifts ##################
#> Numba: 0.01329827 s, detected time shift: 3.15 s, minimal mean distance: 0.084238 s
#> Cython: 0.01338649 s, detected time shift: 3.15 s, minimal mean distance: 0.084238 s
#> Python: 3.06915808 s, detected time shift: 3.15 s, minimal mean distance: 0.084238 s
#>
#> ########## Compare versions for multiple lengths ###########
#> Method 10 100 1000 10000 100000
#> Numba: 0.000157 0.000786 0.013276 0.138520 1.402027In the directory nearest_advocate/experiments, multiple Jupyter Notebooks contain experiments based on data in the data directory.
When using in academic works please cite:
Schranz, C., Mayr, S., Bernhart, S. et al. Nearest advocate: a novel event-based time delay estimation algorithm for multi-sensor time-series data synchronization. EURASIP J. Adv. Signal Process. 2024, 46 (2024). https://doi.org/10.1186/s13634-024-01143-1
or:
Schranz, C., & Mayr, S. (2022, September 29). Ein neuer Algorithmus zur Zeitsynchronisierung von Ereignis- basierten Zeitreihendaten als Alternative zur Kreuzkorrelation. Proceedings of the 14th Symposium of the Section Sport Informatics and Engineering of the German Society of Sport Science (dvs) (spinfortec2022), Chemnitz. https://doi.org/10.5281/zenodo.7370958