-
Notifications
You must be signed in to change notification settings - Fork 72
Commit
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
- Loading branch information
Showing
14 changed files
with
508 additions
and
0 deletions.
There are no files selected for viewing
39 changes: 39 additions & 0 deletions
39
src/main/java/g3201_3300/s3248_snake_in_matrix/Solution.java
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,39 @@ | ||
| package g3201_3300.s3248_snake_in_matrix; | ||
|
|
||
| // #Easy #Array #String #Simulation #2024_08_13_Time_2_ms_(98.05%)_Space_44.4_MB_(66.96%) | ||
|
|
||
| import java.util.List; | ||
|
|
||
| public class Solution { | ||
| public int finalPositionOfSnake(int n, List<String> commands) { | ||
| int x = 0; | ||
| int y = 0; | ||
| for (String command : commands) { | ||
| switch (command) { | ||
| case "UP": | ||
| if (x > 0) { | ||
| x--; | ||
| } | ||
| break; | ||
| case "DOWN": | ||
| if (x < n - 1) { | ||
| x++; | ||
| } | ||
| break; | ||
| case "LEFT": | ||
| if (y > 0) { | ||
| y--; | ||
| } | ||
| break; | ||
| case "RIGHT": | ||
| if (y < n - 1) { | ||
| y++; | ||
| } | ||
| break; | ||
| default: | ||
| break; | ||
| } | ||
| } | ||
| return (x * n) + y; | ||
| } | ||
| } |
Loading
Sorry, something went wrong. Reload?
Sorry, we cannot display this file.
Sorry, this file is invalid so it cannot be displayed.
Loading
Sorry, something went wrong. Reload?
Sorry, we cannot display this file.
Sorry, this file is invalid so it cannot be displayed.
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,38 @@ | ||
| 3248\. Snake in Matrix | ||
|
|
||
| Easy | ||
|
|
||
| There is a snake in an `n x n` matrix `grid` and can move in **four possible directions**. Each cell in the `grid` is identified by the position: `grid[i][j] = (i * n) + j`. | ||
|
|
||
| The snake starts at cell 0 and follows a sequence of commands. | ||
|
|
||
| You are given an integer `n` representing the size of the `grid` and an array of strings `commands` where each `command[i]` is either `"UP"`, `"RIGHT"`, `"DOWN"`, and `"LEFT"`. It's guaranteed that the snake will remain within the `grid` boundaries throughout its movement. | ||
|
|
||
| Return the position of the final cell where the snake ends up after executing `commands`. | ||
|
|
||
| **Example 1:** | ||
|
|
||
| **Input:** n = 2, commands = ["RIGHT","DOWN"] | ||
|
|
||
| **Output:** 3 | ||
|
|
||
| **Explanation:** | ||
|
|
||
|  | ||
|
|
||
| **Example 2:** | ||
|
|
||
| **Input:** n = 3, commands = ["DOWN","RIGHT","UP"] | ||
|
|
||
| **Output:** 1 | ||
|
|
||
| **Explanation:** | ||
|
|
||
|  | ||
|
|
||
| **Constraints:** | ||
|
|
||
| * `2 <= n <= 10` | ||
| * `1 <= commands.length <= 100` | ||
| * `commands` consists only of `"UP"`, `"RIGHT"`, `"DOWN"`, and `"LEFT"`. | ||
| * The input is generated such the snake will not move outside of the boundaries. |
74 changes: 74 additions & 0 deletions
74
src/main/java/g3201_3300/s3249_count_the_number_of_good_nodes/Solution.java
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,74 @@ | ||
| package g3201_3300.s3249_count_the_number_of_good_nodes; | ||
|
|
||
| // #Medium #Tree #Depth_First_Search #2024_08_13_Time_34_ms_(100.00%)_Space_113.9_MB_(90.70%) | ||
|
|
||
| import java.util.ArrayList; | ||
| import java.util.List; | ||
|
|
||
| public class Solution { | ||
| private int count = 0; | ||
|
|
||
| public int countGoodNodes(int[][] edges) { | ||
| int n = edges.length + 1; | ||
| TNode[] nodes = new TNode[n]; | ||
| nodes[0] = new TNode(0); | ||
| for (int[] edge : edges) { | ||
| int a = edge[0]; | ||
| int b = edge[1]; | ||
| if (nodes[b] != null && nodes[a] == null) { | ||
| nodes[a] = new TNode(a); | ||
| nodes[b].children.add(nodes[a]); | ||
| } else { | ||
| if (nodes[a] == null) { | ||
| nodes[a] = new TNode(a); | ||
| } | ||
| if (nodes[b] == null) { | ||
| nodes[b] = new TNode(b); | ||
| } | ||
| nodes[a].children.add(nodes[b]); | ||
| } | ||
| } | ||
| sizeOfTree(nodes[0]); | ||
| return count; | ||
| } | ||
|
|
||
| private int sizeOfTree(TNode node) { | ||
| if (node.size > 0) { | ||
| return node.size; | ||
| } | ||
| List<TNode> children = node.children; | ||
| if (children.isEmpty()) { | ||
| count++; | ||
| node.size = 1; | ||
| return 1; | ||
| } | ||
| int size = sizeOfTree(children.get(0)); | ||
| int sum = size; | ||
| boolean goodNode = true; | ||
| for (int i = 1; i < children.size(); ++i) { | ||
| TNode child = children.get(i); | ||
| if (size != sizeOfTree(child)) { | ||
| goodNode = false; | ||
| } | ||
| sum += sizeOfTree(child); | ||
| } | ||
| if (goodNode) { | ||
| count++; | ||
| } | ||
| sum++; | ||
| node.size = sum; | ||
| return sum; | ||
| } | ||
|
|
||
| private static class TNode { | ||
| int val; | ||
| int size; | ||
| List<TNode> children; | ||
|
|
||
| TNode(int val) { | ||
| this.val = val; | ||
| this.size = -1; | ||
| this.children = new ArrayList<>(); | ||
| } | ||
| } | ||
| } |
55 changes: 55 additions & 0 deletions
55
src/main/java/g3201_3300/s3249_count_the_number_of_good_nodes/readme.md
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,55 @@ | ||
| 3249\. Count the Number of Good Nodes | ||
|
|
||
| Medium | ||
|
|
||
| There is an **undirected** tree with `n` nodes labeled from `0` to `n - 1`, and rooted at node `0`. You are given a 2D integer array `edges` of length `n - 1`, where <code>edges[i] = [a<sub>i</sub>, b<sub>i</sub>]</code> indicates that there is an edge between nodes <code>a<sub>i</sub></code> and <code>b<sub>i</sub></code> in the tree. | ||
|
|
||
| A node is **good** if all the subtrees rooted at its children have the same size. | ||
|
|
||
| Return the number of **good** nodes in the given tree. | ||
|
|
||
| A **subtree** of `treeName` is a tree consisting of a node in `treeName` and all of its descendants. | ||
|
|
||
| **Example 1:** | ||
|
|
||
| **Input:** edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]] | ||
|
|
||
| **Output:** 7 | ||
|
|
||
| **Explanation:** | ||
|
|
||
| 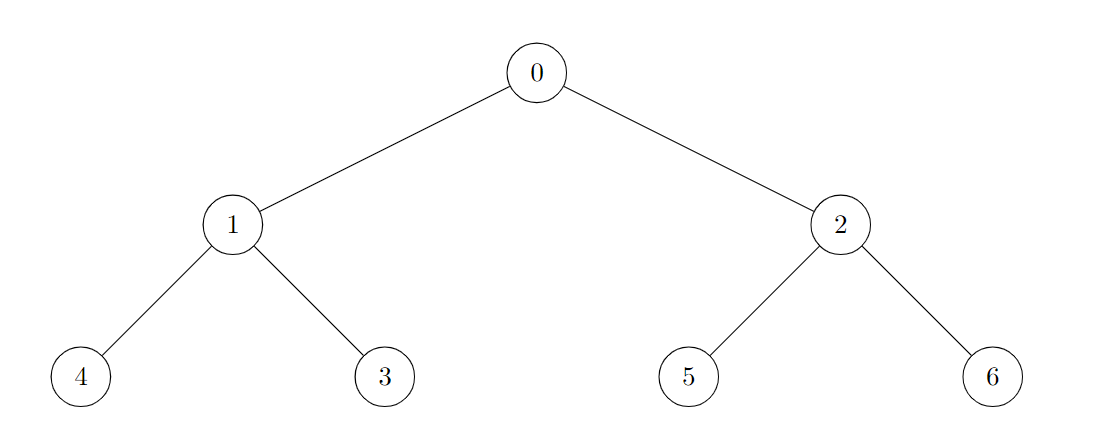 | ||
|
|
||
| All of the nodes of the given tree are good. | ||
|
|
||
| **Example 2:** | ||
|
|
||
| **Input:** edges = [[0,1],[1,2],[2,3],[3,4],[0,5],[1,6],[2,7],[3,8]] | ||
|
|
||
| **Output:** 6 | ||
|
|
||
| **Explanation:** | ||
|
|
||
| 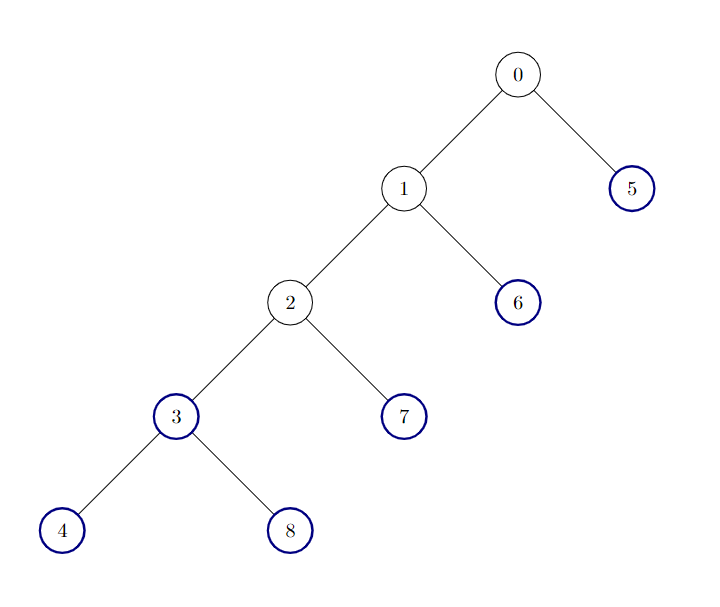 | ||
|
|
||
| There are 6 good nodes in the given tree. They are colored in the image above. | ||
|
|
||
| **Example 3:** | ||
|
|
||
| **Input:** edges = [[0,1],[1,2],[1,3],[1,4],[0,5],[5,6],[6,7],[7,8],[0,9],[9,10],[9,12],[10,11]] | ||
|
|
||
| **Output:** 12 | ||
|
|
||
| **Explanation:** | ||
|
|
||
| 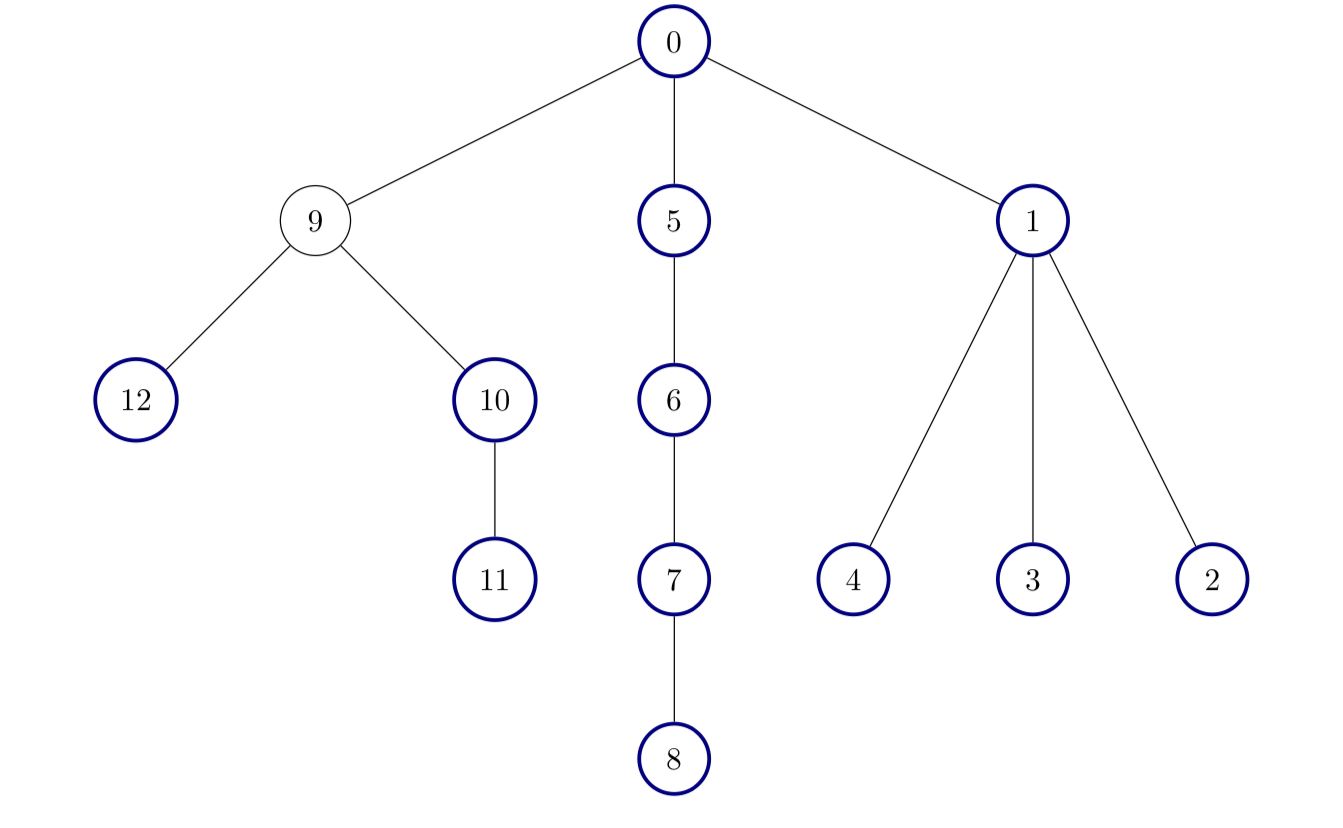 | ||
|
|
||
| All nodes except node 9 are good. | ||
|
|
||
| **Constraints:** | ||
|
|
||
| * <code>2 <= n <= 10<sup>5</sup></code> | ||
| * `edges.length == n - 1` | ||
| * `edges[i].length == 2` | ||
| * <code>0 <= a<sub>i</sub>, b<sub>i</sub> < n</code> | ||
| * The input is generated such that `edges` represents a valid tree. |
43 changes: 43 additions & 0 deletions
43
src/main/java/g3201_3300/s3250_find_the_count_of_monotonic_pairs_i/Solution.java
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,43 @@ | ||
| package g3201_3300.s3250_find_the_count_of_monotonic_pairs_i; | ||
|
|
||
| // #Hard #Array #Dynamic_Programming #Math #Prefix_Sum #Combinatorics | ||
| // #2024_08_13_Time_3_ms_(100.00%)_Space_44.7_MB_(99.34%) | ||
|
|
||
| public class Solution { | ||
| public int countOfPairs(int[] nums) { | ||
| int[] maxShift = new int[nums.length]; | ||
| maxShift[0] = nums[0]; | ||
| int currShift = 0; | ||
| for (int i = 1; i < nums.length; i++) { | ||
| currShift = Math.max(currShift, nums[i] - maxShift[i - 1]); | ||
| maxShift[i] = Math.min(maxShift[i - 1], nums[i] - currShift); | ||
| if (maxShift[i] < 0) { | ||
| return 0; | ||
| } | ||
| } | ||
| int[][] cases = getAllCases(nums, maxShift); | ||
| return cases[nums.length - 1][maxShift[nums.length - 1]]; | ||
| } | ||
|
|
||
| private int[][] getAllCases(int[] nums, int[] maxShift) { | ||
| int[] currCases; | ||
| int[][] cases = new int[nums.length][]; | ||
| cases[0] = new int[maxShift[0] + 1]; | ||
| for (int i = 0; i < cases[0].length; i++) { | ||
| cases[0][i] = i + 1; | ||
| } | ||
| for (int i = 1; i < nums.length; i++) { | ||
| currCases = new int[maxShift[i] + 1]; | ||
| currCases[0] = 1; | ||
| for (int j = 1; j < currCases.length; j++) { | ||
| int prevCases = | ||
| j < cases[i - 1].length | ||
| ? cases[i - 1][j] | ||
| : cases[i - 1][cases[i - 1].length - 1]; | ||
| currCases[j] = (currCases[j - 1] + prevCases) % (1_000_000_000 + 7); | ||
| } | ||
| cases[i] = currCases; | ||
| } | ||
| return cases; | ||
| } | ||
| } |
42 changes: 42 additions & 0 deletions
42
src/main/java/g3201_3300/s3250_find_the_count_of_monotonic_pairs_i/readme.md
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,42 @@ | ||
| 3250\. Find the Count of Monotonic Pairs I | ||
|
|
||
| Hard | ||
|
|
||
| You are given an array of **positive** integers `nums` of length `n`. | ||
|
|
||
| We call a pair of **non-negative** integer arrays `(arr1, arr2)` **monotonic** if: | ||
|
|
||
| * The lengths of both arrays are `n`. | ||
| * `arr1` is monotonically **non-decreasing**, in other words, `arr1[0] <= arr1[1] <= ... <= arr1[n - 1]`. | ||
| * `arr2` is monotonically **non-increasing**, in other words, `arr2[0] >= arr2[1] >= ... >= arr2[n - 1]`. | ||
| * `arr1[i] + arr2[i] == nums[i]` for all `0 <= i <= n - 1`. | ||
|
|
||
| Return the count of **monotonic** pairs. | ||
|
|
||
| Since the answer may be very large, return it **modulo** <code>10<sup>9</sup> + 7</code>. | ||
|
|
||
| **Example 1:** | ||
|
|
||
| **Input:** nums = [2,3,2] | ||
|
|
||
| **Output:** 4 | ||
|
|
||
| **Explanation:** | ||
|
|
||
| The good pairs are: | ||
|
|
||
| 1. `([0, 1, 1], [2, 2, 1])` | ||
| 2. `([0, 1, 2], [2, 2, 0])` | ||
| 3. `([0, 2, 2], [2, 1, 0])` | ||
| 4. `([1, 2, 2], [1, 1, 0])` | ||
|
|
||
| **Example 2:** | ||
|
|
||
| **Input:** nums = [5,5,5,5] | ||
|
|
||
| **Output:** 126 | ||
|
|
||
| **Constraints:** | ||
|
|
||
| * `1 <= n == nums.length <= 2000` | ||
| * `1 <= nums[i] <= 50` |
34 changes: 34 additions & 0 deletions
34
src/main/java/g3201_3300/s3251_find_the_count_of_monotonic_pairs_ii/Solution.java
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,34 @@ | ||
| package g3201_3300.s3251_find_the_count_of_monotonic_pairs_ii; | ||
|
|
||
| // #Hard #Array #Dynamic_Programming #Math #Prefix_Sum #Combinatorics | ||
| // #2024_08_13_Time_24_ms_(100.00%)_Space_44.7_MB_(97.70%) | ||
|
|
||
| import java.util.Arrays; | ||
|
|
||
| public class Solution { | ||
| private static final int MOD = 1000000007; | ||
|
|
||
| public int countOfPairs(int[] nums) { | ||
| int prefixZeros = 0; | ||
| int n = nums.length; | ||
| // Calculate prefix zeros | ||
| for (int i = 1; i < n; i++) { | ||
| prefixZeros += Math.max(nums[i] - nums[i - 1], 0); | ||
| } | ||
| int row = n + 1; | ||
| int col = nums[n - 1] + 1 - prefixZeros; | ||
| if (col <= 0) { | ||
| return 0; | ||
| } | ||
| // Initialize dp array | ||
| int[] dp = new int[col]; | ||
| Arrays.fill(dp, 1); | ||
| // Fill dp array | ||
| for (int r = 1; r < row; r++) { | ||
| for (int c = 1; c < col; c++) { | ||
| dp[c] = (dp[c] + dp[c - 1]) % MOD; | ||
| } | ||
| } | ||
| return dp[col - 1]; | ||
| } | ||
| } |
42 changes: 42 additions & 0 deletions
42
src/main/java/g3201_3300/s3251_find_the_count_of_monotonic_pairs_ii/readme.md
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,42 @@ | ||
| 3251\. Find the Count of Monotonic Pairs II | ||
|
|
||
| Hard | ||
|
|
||
| You are given an array of **positive** integers `nums` of length `n`. | ||
|
|
||
| We call a pair of **non-negative** integer arrays `(arr1, arr2)` **monotonic** if: | ||
|
|
||
| * The lengths of both arrays are `n`. | ||
| * `arr1` is monotonically **non-decreasing**, in other words, `arr1[0] <= arr1[1] <= ... <= arr1[n - 1]`. | ||
| * `arr2` is monotonically **non-increasing**, in other words, `arr2[0] >= arr2[1] >= ... >= arr2[n - 1]`. | ||
| * `arr1[i] + arr2[i] == nums[i]` for all `0 <= i <= n - 1`. | ||
|
|
||
| Return the count of **monotonic** pairs. | ||
|
|
||
| Since the answer may be very large, return it **modulo** <code>10<sup>9</sup> + 7</code>. | ||
|
|
||
| **Example 1:** | ||
|
|
||
| **Input:** nums = [2,3,2] | ||
|
|
||
| **Output:** 4 | ||
|
|
||
| **Explanation:** | ||
|
|
||
| The good pairs are: | ||
|
|
||
| 1. `([0, 1, 1], [2, 2, 1])` | ||
| 2. `([0, 1, 2], [2, 2, 0])` | ||
| 3. `([0, 2, 2], [2, 1, 0])` | ||
| 4. `([1, 2, 2], [1, 1, 0])` | ||
|
|
||
| **Example 2:** | ||
|
|
||
| **Input:** nums = [5,5,5,5] | ||
|
|
||
| **Output:** 126 | ||
|
|
||
| **Constraints:** | ||
|
|
||
| * `1 <= n == nums.length <= 2000` | ||
| * `1 <= nums[i] <= 1000` |
Oops, something went wrong.