CorrCount (R implementation)

EM Algorithm for Correlated Count Data with Hidden Segments (used to cluster shopping data)

Problem

Suppose we collected data on all items purchased by our customers during a fixed time period.

For each item, we have its category, price, and shopper id. We could display these data in the following pivot table:

 Purchases (Grouped by Shopper and by Category)
+==============================================================+
| Shopper ID | Category1 | Category2 | Category 3 | Cetegory 4 |
+============+===========+===========+============+============+
| 1          | $39.95    |           | $15.45     |            |
|            | $31.05    |           | $14.06     |            |
|            | $28.49    |           |            |            |
|            | $58.98    |           |            |            |
|            |           |           |            |            |
| 2          | $15.49    | $109.34   | $16.95     | $98.50     |
|            |           | $156.00   | $16.95     |            |
|            |           |  $99.12   |            |            |
|            |           | $109.34   |            |            |
| 3          | $19.99    |           |            | $74.50     |
|            | $39.99    |           |            | $81.95     |
|            | $19.99    |           |            |            |
|            | $21.50    |           |            |            |
|            | $29.75    |           |            |            |
|    ...     |    ...    |    ...    |     ...    |     ...    |
+============+===========+===========+============+============+

Our goal is to find segments in our customer base, so that customers from the same segment have similar purchasing behaviour (similar purchase counts and amounts per category), while customers from different segments have different purchasing behaviour.

We can quantify user 's "preference" for category by looking at the expected purchase frequency (count) made by the user in that category, as well as the average purchase amount made by the same user in the same category (provided, of course, that is non-zero.

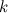
Suppose that there are S "hidden" (unobserved) customer segments, so that for any customer the following holds:

So we need to figure out the number of hidden segments, find segment means (counts and amounts), and finally classify each customer into one of the segments. Then we will be able to make revenue predictions and develop targeted campaigns for each segment.

We will use a probability model. However, we should take into account the following basic feature:

• Category frequencies for the same user are correlated. If we ingored this, then it would be much easier to find the segments and estimate the means, but the results would be really bad at predictions because a model without correlations is unrealistic.

Model

The goal is to fit our data with the following Bayesian Network model:

[INSERT IMG FROM DAFT]

[TODO]

Usage Examples

[TODO]