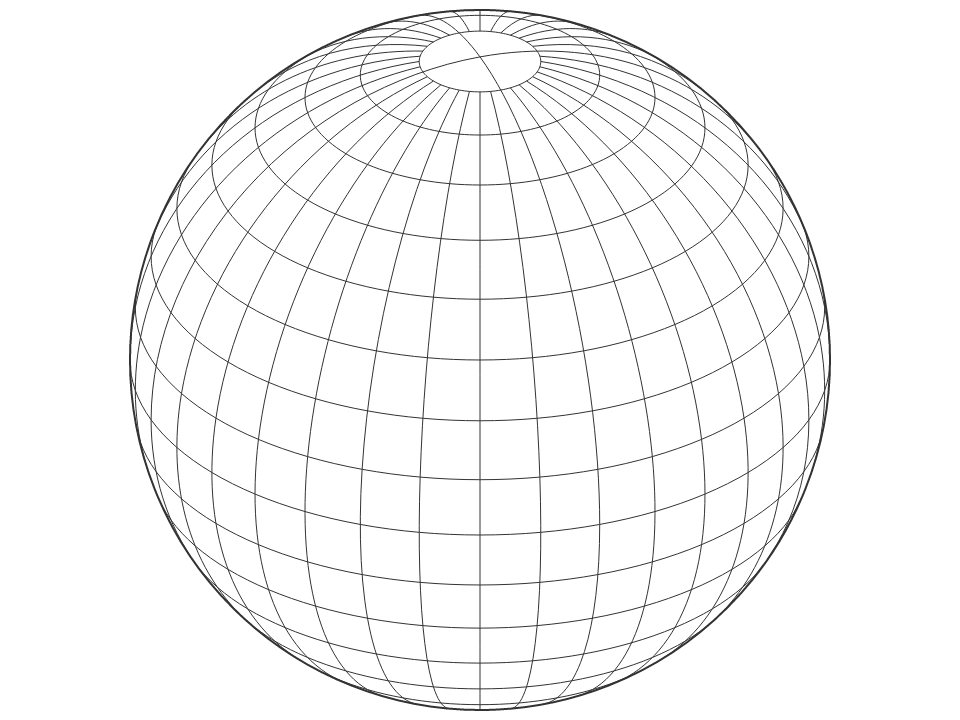
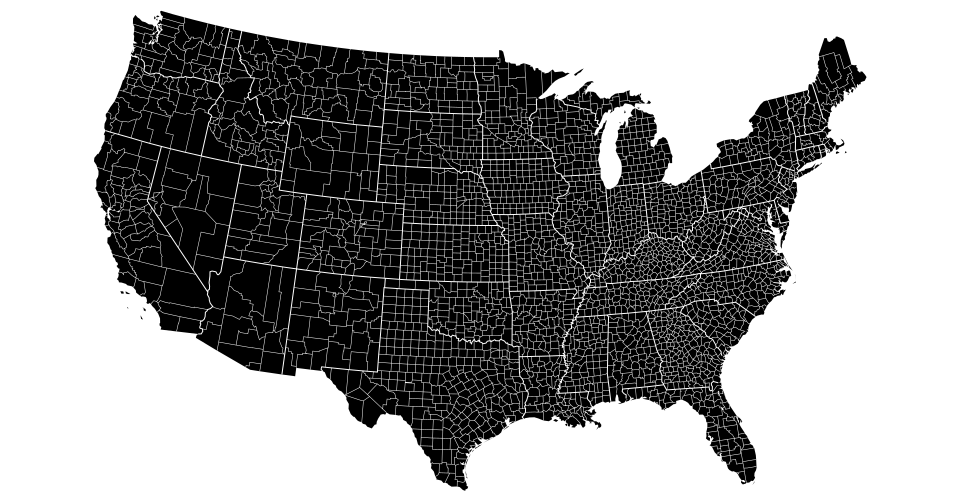
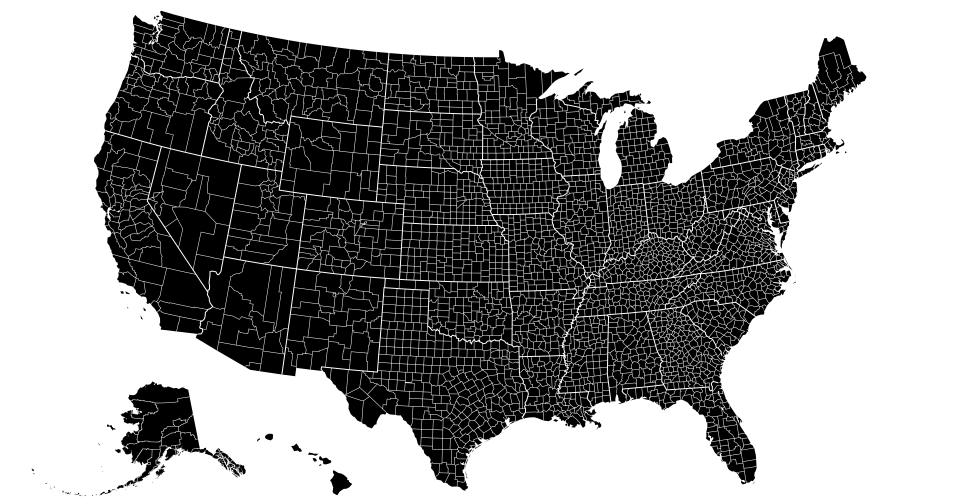
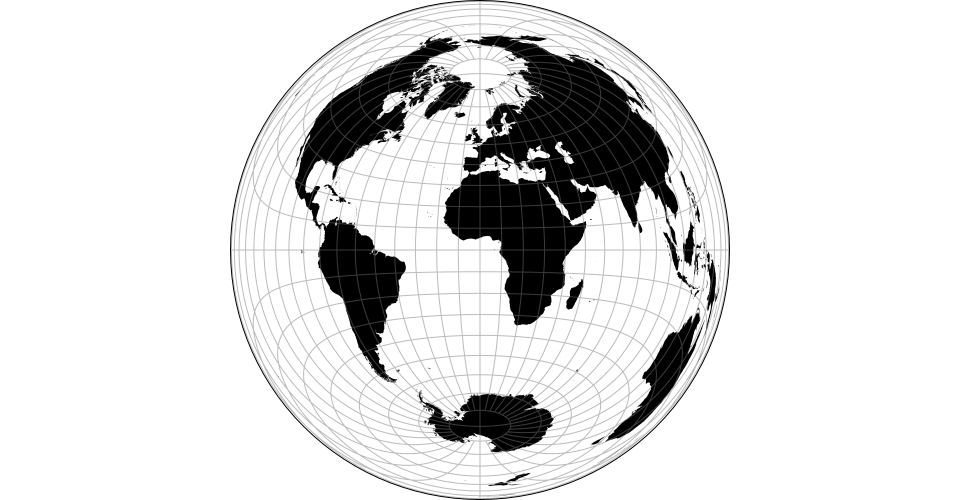
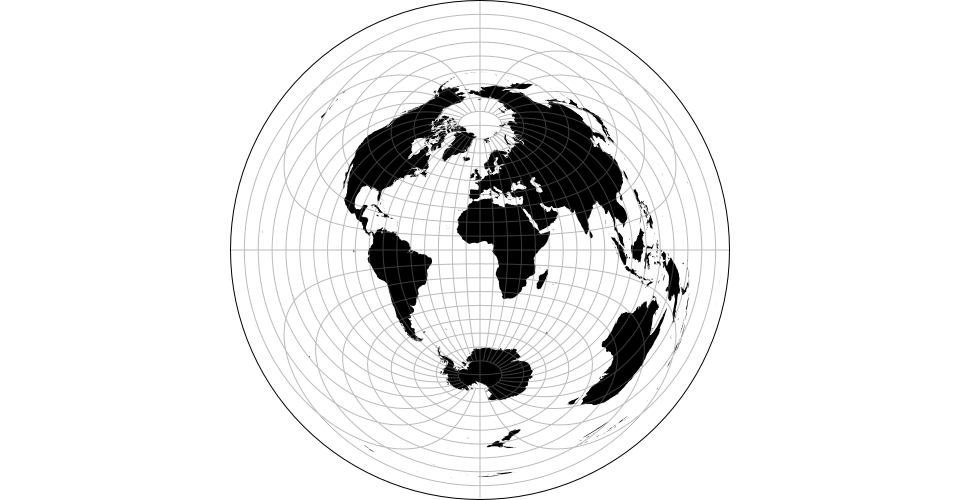
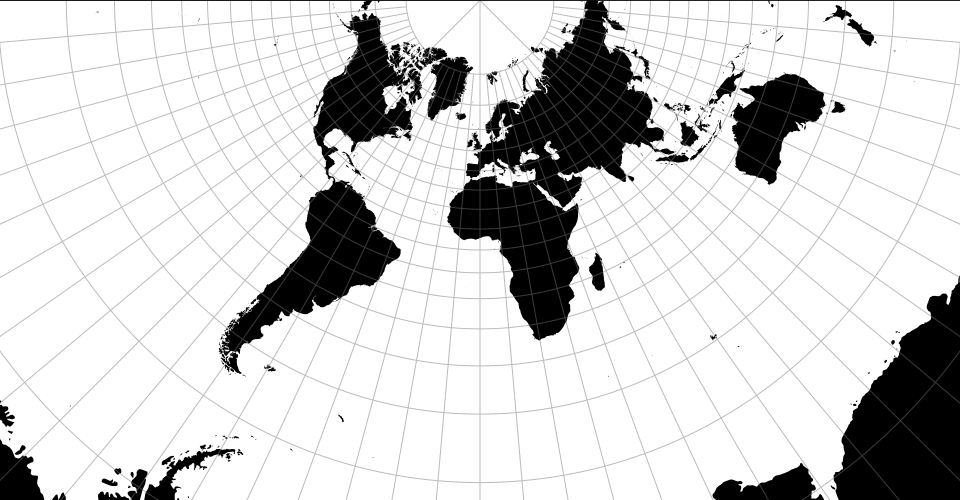
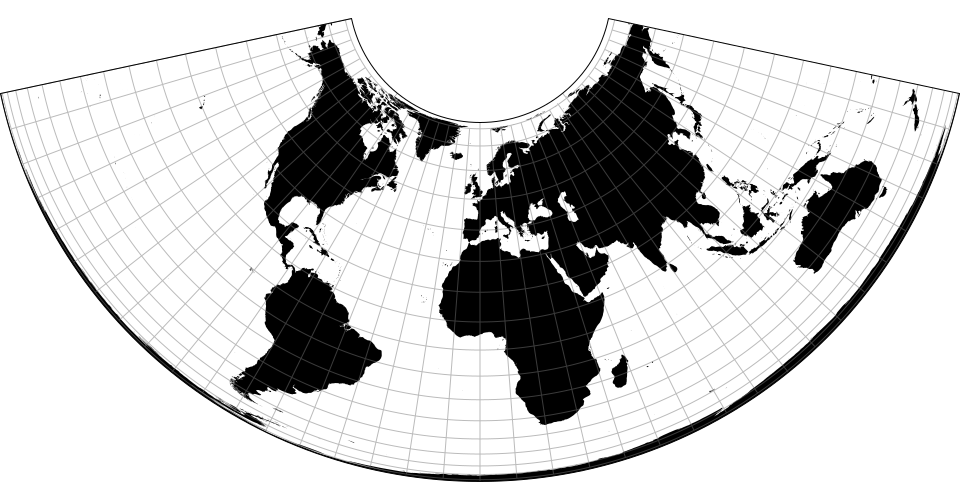
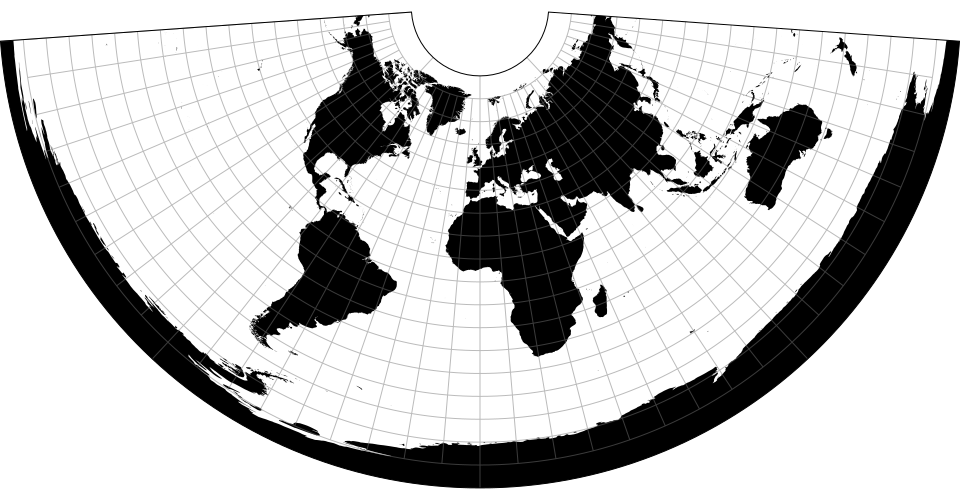
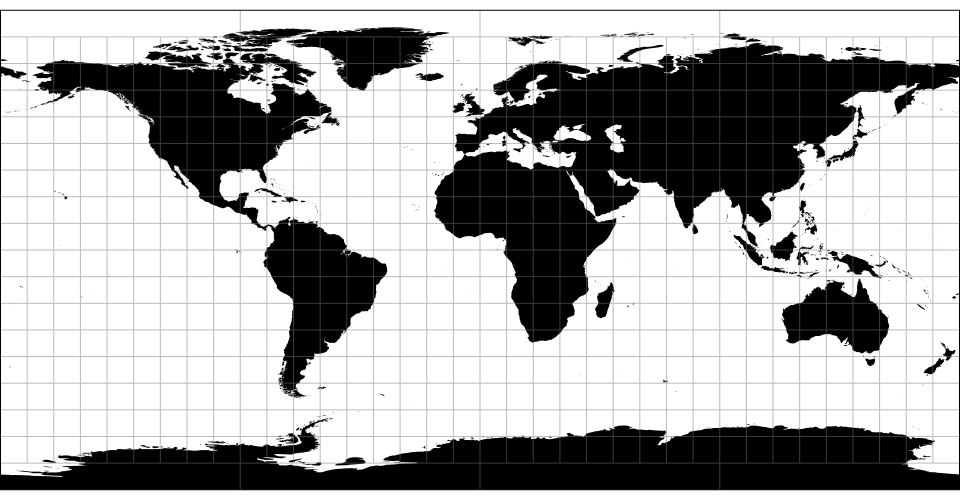
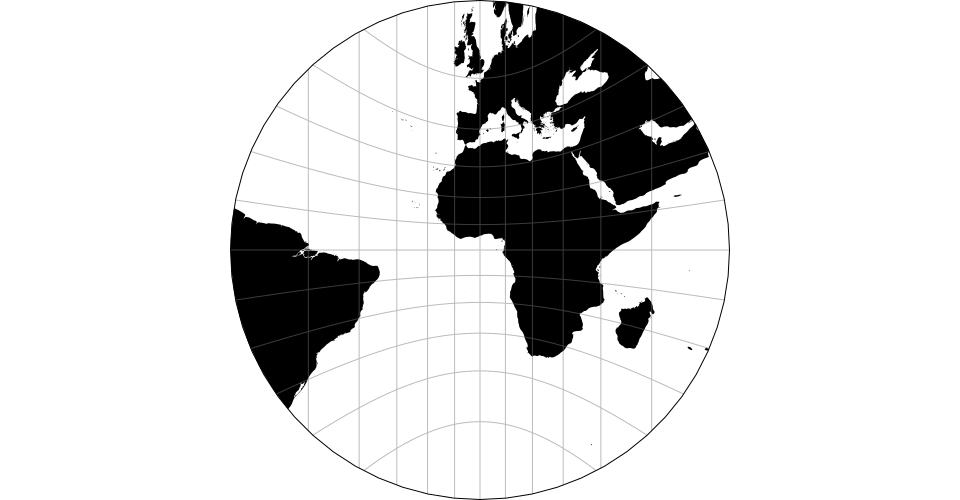
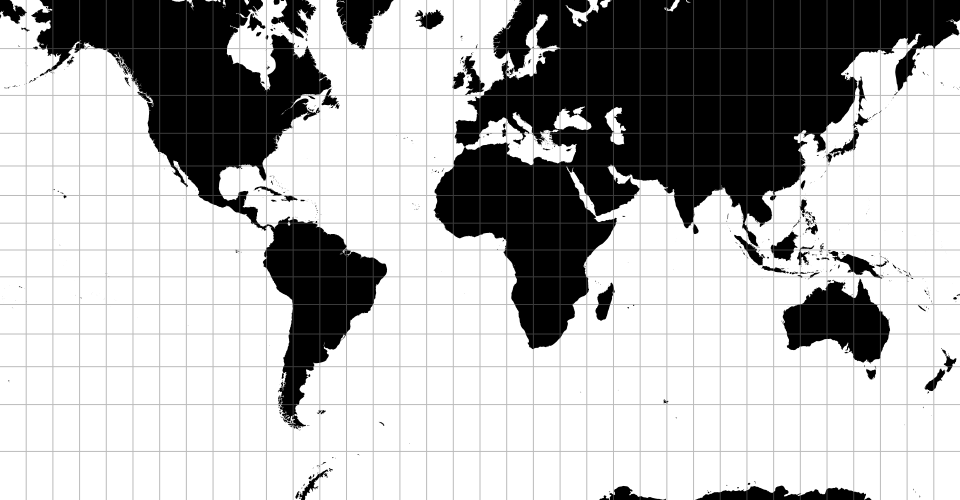
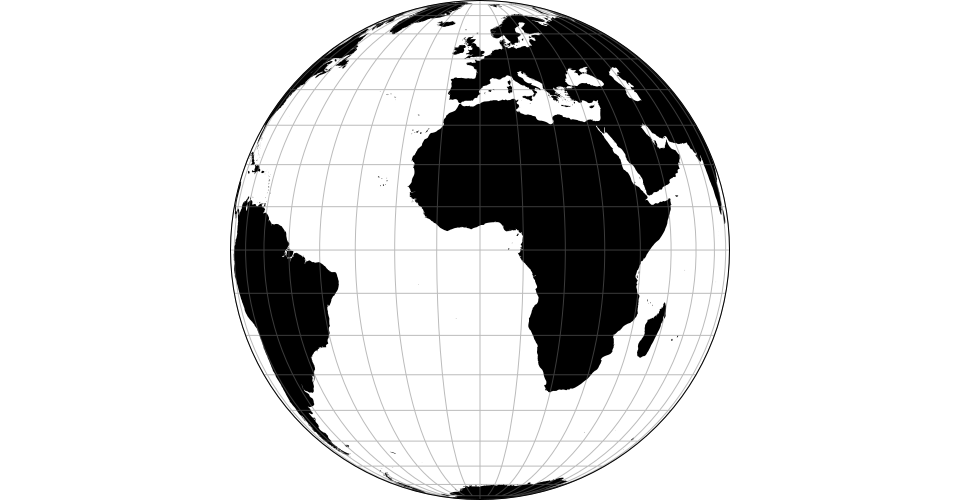
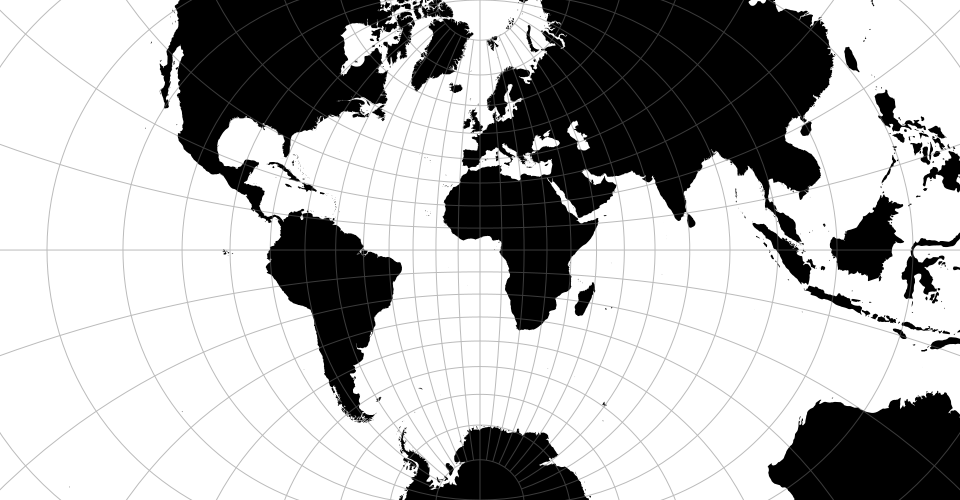
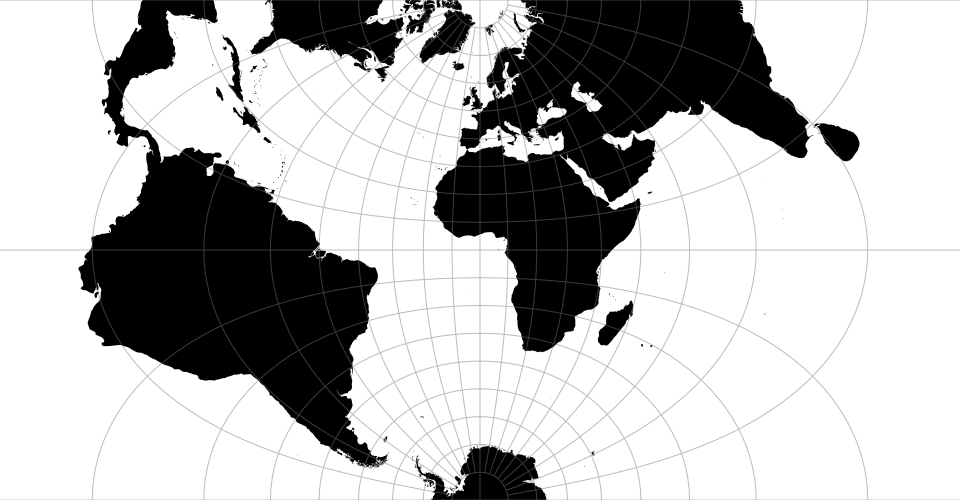
Map projections are often naïvely regarded as simple point transformations. Spherical Mercator, for instance, can be implemented concisely as:
function mercator(x, y) {
return [x, Math.log(Math.tan(Math.PI / 4 + y / 2))];
}While this is a reasonable mathematical representation, it only works if your geometry is represented continuously as infinite point sets! Of course computers do not have infinite memory, and so we must instead work with discrete geometry such as polygons and polylines.
Alas, discrete geometry makes the challenge of projecting from the sphere to the plane much harder. The edges of a spherical polygon are geodesics (also known as great arcs, or segments of a great circle), not straight lines. Even projected to the plane, geodesics remain curves in all map projections except gnomonic, and thus accurate projection requires interpolating along great arcs. D3 uses adaptive interpolation, inspired by a popular line simplification method, to balance accuracy and performance.
The projection of polygons and polylines must also deal with the topological differences between the sphere and the plane. Some projections require cutting geometry that cross the antimeridian, while others require clipping geometry to a great circle. Furthermore, spherical polygons require a winding order convention to determine which side of the polygon is the inside: D3 and TopoJSON use clockwise winding. (Spherical polygons can be larger than a hemisphere! See also ST_ForceRHR in PostGIS.)
D3’s approach affords great expressiveness: you can choose the right projection, and the right aspect, for your data. D3 supports a wide variety of common and unusual map projections. For more, see Part 2 of The Toolmaker’s Guide.
D3 uses GeoJSON to represent geographic features in JavaScript. (See also TopoJSON, an extension of GeoJSON that is significantly more compact and encodes topology.) To convert shapefiles to GeoJSON, use ogr2ogr, part of the GDAL package. In addition to map projections, D3 includes useful spherical shape generators and spherical math utilities.
If you use NPM, npm install d3-geo. Otherwise, download the latest release. You can also load directly from d3js.org, either as a standalone library or as part of D3 4.0. AMD, CommonJS, and vanilla environments are supported. In vanilla, a d3 global is exported:
<script src="https://d3js.org/d3-array.v1.min.js"></script>
<script src="https://d3js.org/d3-geo.v1.min.js"></script>
<script>
var path = d3.geoPath();
</script># d3.geoArea(feature)
Returns the spherical area of the specified GeoJSON feature in steradians. See also path.area, which computes the projected planar area.
# d3.geoBounds(feature)
Returns the spherical bounding box for the specified GeoJSON feature. The bounding box is represented by a two-dimensional array: [[left, bottom], [right, top]], where left is the minimum longitude, bottom is the minimum latitude, right is maximum longitude, and top is the maximum latitude. All coordinates are given in degrees. (Note that in projected planar coordinates, the minimum latitude is typically the maximum y-value, and the maximum latitude is typically the minimum y-value.)
# d3.geoCentroid(feature)
Returns the spherical centroid of the specified GeoJSON feature. See also path.centroid, which computes the projected planar centroid.
# d3.geoDistance(a, b)
Returns the great-arc distance in radians between the two points a and b. Each point must be specified as a two-element array [longitude, latitude] in degrees.
# d3.geoLength(feature)
Returns the great-arc length of the specified GeoJSON feature in radians. For polygons, returns the perimeter of the exterior ring plus that of any interior rings.
# d3.geoInterpolate(a, b)
Returns an interpolator function given two points a and b. Each point must be specified as a two-element array [longitude, latitude] in degrees. The returned interpolator function takes a single argument t, where t is a number ranging from 0 to 1; a value of 0 returns the point a, while a value of 1 returns the point b. Intermediate values interpolate from a to b along the great arc that passes through both a and b. If a and b are antipodes, an arbitrary great arc is chosen.
# d3.geoRotation(angles)
Returns a rotation function for the given angles, which must be a two- or three-element array of numbers [lambda, phi, gamma] specifying the rotation angles in degrees about each spherical axis. (These correspond to yaw, pitch and roll.) If the rotation angle gamma is omitted, it defaults to 0. See also projection.rotate.
# rotation(point)
Returns a new array [longitude, latitude] in degrees representing the rotated point of the given point. The point must be specified as a two-element array [longitude, latitude] in degrees.
# rotation.invert(point)
Returns a new array [longitude, latitude] in degrees representing the point of the given rotated point; the inverse of rotation. The point must be specified as a two-element array [longitude, latitude] in degrees.
To generate a great arc (a segment of a great circle), simply pass a GeoJSON LineString geometry object to a d3.geoPath. D3’s projections use great-arc interpolation for intermediate points, so there’s no need for a great arc shape generator.
# d3.geoCircle()
Returns a new circle generator.
# circle(arguments…)
Returns a new GeoJSON geometry object of type “Polygon” approximating a circle on the surface of a sphere, with the current center, radius and precision. Any arguments are passed to the accessors.
# circle.center([center])
If center is specified, sets the circle center to the specified point [longitude, latitude] in degrees, and returns this circle generator. The center may also be specified as a function; this function will be invoked whenever a circle is generated, being passed any arguments passed to the circle generator. If center is not specified, returns the current center accessor, which defaults to:
function center() {
return [0, 0];
}# circle.radius([radius])
If radius is specified, sets the circle radius to the specified angle in degrees, and returns this circle generator. The radius may also be specified as a function; this function will be invoked whenever a circle is generated, being passed any arguments passed to the circle generator. If radius is not specified, returns the current radius accessor, which defaults to:
function radius() {
return 90;
}# circle.precision([angle])
If precision is specified, sets the circle precision to the specified angle in degrees, and returns this circle generator. The precision may also be specified as a function; this function will be invoked whenever a circle is generated, being passed any arguments passed to the circle generator. If precision is not specified, returns the current precision accessor, which defaults to:
function precision() {
return 6;
}Small circles do not follow great arcs and thus the generated polygon is only an approximation. Specifying a smaller precision angle improves the accuracy of the approximate polygon, but also increase the cost to generate and render it.
# d3.geoGraticule()
Constructs a feature generator for creating graticules: a uniform grid of meridians and parallels for showing projection distortion. The default graticule has meridians and parallels every 10° between ±80° latitude; for the polar regions, there are meridians every 90°.
# graticule()
Returns a GeoJSON MultiLineString geometry object representing all meridians and parallels for this graticule.
# graticule.lines()
Returns an array of GeoJSON LineString geometry objects, one for each meridian or parallel for this graticule.
# graticule.outline()
Returns a GeoJSON Polygon geometry object representing the outline of this graticule, i.e. along the meridians and parallels defining its extent.
# graticule.extent([extent])
If extent is specified, sets the major and minor extents of this graticule. If extent is not specified, returns the current minor extent, which defaults to ⟨⟨-180°, -80° - ε⟩, ⟨180°, 80° + ε⟩⟩.
# graticule.extentMajor([extent])
If extent is specified, sets the major extent of this graticule. If extent is not specified, returns the current major extent, which defaults to ⟨⟨-180°, -90° + ε⟩, ⟨180°, 90° - ε⟩⟩.
# graticule.extentMinor([extent])
If extent is specified, sets the minor extent of this graticule. If extent is not specified, returns the current minor extent, which defaults to ⟨⟨-180°, -80° - ε⟩, ⟨180°, 80° + ε⟩⟩.
# graticule.step([step])
If step is specified, sets the major and minor step for this graticule. If step is not specified, returns the current minor step, which defaults to ⟨10°, 10°⟩.
# graticule.stepMajor([step])
If step is specified, sets the major step for this graticule. If step is not specified, returns the current major step, which defaults to ⟨90°, 360°⟩.
# graticule.stepMinor([step])
If step is specified, sets the minor step for this graticule. If step is not specified, returns the current minor step, which defaults to ⟨10°, 10°⟩.
# graticule.precision([angle])
If precision is specified, sets the precision for this graticule, in degrees. If precision is not specified, returns the current precision, which defaults to 2.5°.
The geographic path generator, d3.geoPath, is similar to the shape generators in d3-shape: given a GeoJSON geometry or feature object, it generates an SVG path data string or renders the path to a Canvas. Canvas is recommended for dynamic or interactive projections to improve performance.
# d3.geoPath()
Creates a new geographic path generator with the default settings.
# path(object[, arguments…])
Renders the given object, which may be any GeoJSON feature or geometry object:
- Point - a single position.
- MultiPoint - an array of positions.
- LineString - an array of positions forming a continuous line.
- MultiLineString - an array of arrays of positions forming several lines.
- Polygon - an array of arrays of positions forming a polygon (possibly with holes).
- MultiPolygon - a multidimensional array of positions forming multiple polygons.
- GeometryCollection - an array of geometry objects.
- Feature - a feature containing one of the above geometry objects.
- FeatureCollection - an array of feature objects.
The type Sphere is also supported, which is useful for rendering the outline of the globe; a sphere has no coordinates. Any additional arguments are passed along to the pointRadius accessor.
To display multiple features, combine them into a feature collection:
svg.append("path")
.datum({type: "FeatureCollection", features: features})
.attr("d", d3.geoPath());Or use multiple path elements:
svg.selectAll("path")
.data(features)
.enter().append("path")
.attr("d", d3.geoPath());Separate path elements are typically slower than a single path element. However, distinct path elements are useful for styling and interation (e.g., click or mouseover). Canvas rendering (see path.context) is typically faster than SVG, but requires more effort to implement styling and interaction.
# path.area(object)
Returns the projected planar area (typically in square pixels) for the specified GeoJSON object. Point, MultiPoint, LineString and MultiLineString features have zero area. For Polygon and MultiPolygon features, this method first computes the area of the exterior ring, and then subtracts the area of any interior holes. This method observes any clipping performed by the projection; see projection.clipAngle and projection.clipExtent.
# path.bounds(object)
Returns the projected planar bounding box (typically in pixels) for the specified GeoJSON object. The bounding box is represented by a two-dimensional array: [[x₀, y₀], [x₁, y₁]], where x₀ is the minimum x-coordinate, y₀ is the minimum y-coordinate, x₁ is maximum x-coordinate, and y₁ is the maximum y-coordinate. This is handy for, say, zooming in to a particular feature. (Note that in projected planar coordinates, the minimum latitude is typically the maximum y-value, and the maximum latitude is typically the minimum y-value.) This method observes any clipping performed by the projection; see projection.clipAngle and projection.clipExtent.
# path.centroid(object)
Returns the projected planar centroid (typically in pixels) for the specified GeoJSON object. This is handy for, say, labeling state or county boundaries, or displaying a symbol map. For example, a noncontiguous cartogram might scale each state around its centroid. This method observes any clipping performed by the projection; see projection.clipAngle and projection.clipExtent.
# path.projection([projection])
If a projection is specified, sets the current projection to the specified projection. If projection is not specified, returns the current projection, which defaults to null. The null projection represents the identity transformation: the input geometry is not projected and is instead rendered directly in raw coordinates. This can be useful for fast rendering of pre-projected geometry, or for fast rendering of the equirectangular projection.
The given projection is typically one of D3’s built-in geographic projections; however, any object that exposes a projection.stream function can be used, enabling the use of custom projections.
# path.context([context])
If context is specified, sets the current render context and returns the path generator. If the context is null, then the path generator will return an SVG path string; if the context is non-null, the path generator will instead call methods on the specified context to render geometry. The context must implement the following subset of the CavnasRenderingContext2D API:
- context.beginPath()
- context.moveTo(x, y)
- context.lineTo(x, y)
- context.arc(x, y, radius, startAngle, endAngle)
- context.closePath()
If a context is not specified, returns the current render context which defaults to null.
# path.pointRadius([radius])
If radius is specified, sets the radius used to display Point and MultiPoint features to the specified number. If radius is not specified, returns the current radius accessor, which defaults to 4.5. While the radius is commonly specified as a number constant, it may also be specified as a function which is computed per feature, being passed the any arguments passed to the path generator. For example, if your GeoJSON data has additional properties, you might access those properties inside the radius function to vary the point size; alternatively, you could d3.symbol and a projection for greater flexibility.
# d3.geoProjection(project)
Constructs a new projection from the specified raw projection, project. The project function takes the longitude and latitude of a given point in radians, often referred to as lambda (λ) and phi (φ), and returns a two-element array [x, y] representing its unit projection. The project function does not need to scale or translate the point, as these are applied automatically by projection.scale, projection.translate, and projection.center. Likewise, the project function does not need to perform any spherical rotation, as projection.rotate is applied prior to projection.
For example, a spherical Mercator projection can be implemented as:
var mercator = d3.geoProjection(function(x, y) {
return [x, Math.log(Math.tan(Math.PI / 4 + y / 2))];
});If the project function exposes an invert method, the returned projection will also expose projection.invert.
# d3.geoProjectionMutator(factory)
Constructs a new projection from the specified raw projection factory and returns a mutate function to call whenever the raw projection function changes. The factory must return a raw projection. The returned mutate function returns the wrapped projection. For example, a conic projection typically has two configurable parallels. A suitable factory function would be:
// y0 and y1 represent two parallels
function conicFactory(phi0, phi1) {
return function conicRaw(lambda, phi) {
return […, …];
};
}Using d3.geoProjectionMutator, you can implement a standard projection that allows the parallels to be changed, reassigning the raw projection used internally by d3.geoProjection:
function conicCustom() {
var phi0 = 29.5,
phi1 = 45.5,
mutate = d3.geoProjectionMutator(conicFactory),
projection = mutate(phi0, phi1);
projection.parallels = function(_) {
return arguments.length ? mutate(phi0 = +_[0], phi1 = +_[1]) : [phi0, phi1];
};
return projection;
}When creating a mutable projection, the mutate function is typically not exposed.
# projection(point)
Returns a new array [x, y] (typically in pixels) representing the projected point of the given point. The point must be specified as a two-element array [longitude, latitude] in degrees. May return null if the specified point has no defined projected position, such as when the point is outside the clipping bounds of the projection.
# projection.invert(point)
Returns a new array [longitude, latitude] in degrees representing the unprojected point of the given projected point. The point must be specified as a two-element array [x, y] (typically in pixels). May return null if the specified point has no defined projected position, such as when the point is outside the clipping bounds of the projection.
This method is only defined on invertible projections.
# projection.stream(stream)
Returns a projection stream for the specified output stream. Any input geometry is projected before being streamed to the output stream. A typical projection involves several geometry transformations: the input geometry is first converted to radians, rotated on three axes, clipped to the small circle or cut along the antimeridian, and lastly projected to the plane with adaptive resampling, scale and translation.
# projection.clipAngle([angle])
If angle is specified, sets the projection’s clipping circle radius to the specified angle in degrees and returns the projection. If angle is null, switches to antimeridian cutting rather than small-circle clipping. If angle is not specified, returns the current clip angle which defaults to null. Small-circle clipping is independent of viewport clipping via projection.clipExtent.
# projection.clipExtent([extent])
If extent is specified, sets the projection’s viewport clip extent to the specified bounds in pixels and returns the projection. The extent bounds are specified as an array [[x₀, y₀], [x₁, y₁]], where x₀ is the left-side of the viewport, y₀ is the top, x₁ is the right and y₁ is the bottom. If extent is null, no viewport clipping is performed. If extent is not specified, returns the current viewport clip extent which defaults to null. Viewport clipping is independent of small-circle clipping via projection.clipAngle.
# projection.scale([scale])
If scale is specified, sets the projection’s scale factor to the specified value and returns the projection. If scale is not specified, returns the current scale factor; the default scale is projection-specific. The scale factor corresponds linearly to the distance between projected points; however, absolute scale factors are not equivalent across projections.
# projection.translate([translate])
If translate is specified, sets the projection’s translation offset to the specified two-element array [tx, ty] and returns the projection. If translate is not specified, returns the current translation offset which defaults to [480, 250]. The translation offset determines the pixel coordinates of the projection’s center. The default translation offset places ⟨0°,0°⟩ at the center of a 960×500 area.
# projection.center([center])
If center is specified, sets the projection’s center to the specified center, a two-element array of longitude and latitude in degrees and returns the projection. If center is not specified, returns the current center, which defaults to ⟨0°,0°⟩.
# projection.rotate([angles])
If rotation is specified, sets the projection’s three-axis rotation to the specified angles, which must be a two- or three-element array of numbers [lambda, phi, gamma] specifying the rotation angles in degrees about each spherical axis. (These correspond to yaw, pitch and roll.) If the rotation angle gamma is omitted, it defaults to 0. See also d3.geoRotation. If rotation is not specified, returns the current rotation which defaults [0, 0, 0].
# projection.precision([precision])
If precision is specified, sets the threshold for the projection’s adaptive resampling to the specified value in pixels and returns the projection. This value corresponds to the Douglas–Peucker distance. If precision is not specified, returns the projection’s current resampling precision which defaults to √0.5 ≅ 0.70710…
# d3.geoAlbers()
The Albers’ equal area-conic projection. This is a U.S.-centric configuration of d3.geoConicEqualArea.
# d3.geoAlbersUsa()
This is a U.S.-centric composite projection of three d3.geoConicEqualArea projections: d3.geoAlbers is used for the lower forty-eight states, and separate conic equal-area projections are used for Alaska and Hawaii. Note that the scale for Alaska is diminished: it is projected at 0.35× its true relative area.
# d3.geoAzimuthalEqualArea()
The azimuthal equal-area projection.
# d3.geoAzimuthalEquidistant()
The azimuthal equidistant projection.
# d3.geoConicConformal()
The conic conformal projection. The parallels default to [30°, 30°] resulting in flat top. See also conic.parallels.
# d3.geoConicEqualArea()
The Albers’ equal-area conic projection. See also conic.parallels.
# d3.geoConicEquidistant()
The conic equidistant projection. See also conic.parallels.
# d3.geoEquirectangular()
The equirectangular (plate carrée) projection.
# d3.geoGnomonic()
The gnomonic projection.
# d3.geoMercator()
The spherical Mercator projection. Defines a default projection.clipExtent such that the world is projected to a square, clipped to approximately ±85° latitude.
# d3.geoOrthographic()
The orthographic projection.
# d3.geoStereographic()
The stereographic projection.
# d3.geoTransverseMercator()
The transverse spherical Mercator projection. Defines a default projection.clipExtent such that the world is projected to a square, clipped to approximately ±85° latitude.
# conic.parallels([parallels])
…
# d3.geoClipExtent()
…
# extent.extent([extent])
…
# extent.stream(stream)
… See projection.stream.
Raw projections are used to implement projections; they typically passed to d3.geoProjection or d3.geoProjectionMutator. They are exposed here to facilitate the derivation of related projections. Raw projections define simple point transformations: they take spherical coordinates [lambda, phi] in radians and return a point [x, y], typically in the unit square centered around the origin.
# project(lambda, phi)
Projects the specified point [lambda, phi] in radians, returning a new point [x, y] in unitless coordinates.
# project.invert(x, y)
The inverse of project.
# d3.geoAzimuthalEqualAreaRaw
# d3.geoAzimuthalEquidistantRaw
# d3.geoConicConformalRaw(phi0, phi1)
# d3.geoConicEqualAreaRaw(phi0, phi1)
# d3.geoConicEquidistantRaw(phi0, phi1)
# d3.geoEquirectangularRaw
# d3.geoGnomonicRaw
# d3.geoMercatorRaw
# d3.geoOrthographicRaw
# d3.geoStereographicRaw
# d3.geoTransverseMercatorRaw
Yadda yadda some introduction about how D3 transforms geometry using sequences of function calls to minimize the overhead of intermediate representations… Despite the name “stream”, these method calls are currently synchronous.
Streams must implement several methods to receive input geometry. Streams are inherently stateful; the meaning of a point depends on whether the point is inside of a line, and likewise a line is distinguished from a ring by a polygon.
# stream.point(x, y[, z])
Indicates a point with the specified coordinates x and y (and optionally z). The coordinate system is unspecified and implementation-dependent; for example, projection streams require spherical coordinates in degrees as input. Outside the context of a polygon or line, a point indicates a point geometry object (Point or MultiPoint). Within a line or polygon ring, the point indicates a control point.
# stream.lineStart()
Indicates the start of a line or ring. Within a polygon, indicates the start of a ring. The first ring of a polygon is the exterior ring, and is typically clockwise. Any subsequent rings indicate holes in the polygon, and are typically counterclockwise.
# stream.lineEnd()
Indicates the end of a line or ring. Within a polygon, indicates the end of a ring. Unlike GeoJSON, the redundant closing coordinate of a ring is not indicated via point, and instead is implied via lineEnd within a polygon. Thus, the given polygon input:
{
"type": "Polygon",
"coordinates": [
[[0, 0], [1, 0], [1, 1], [0, 1], [0, 0]]
]
}Will produce the following series of method calls on the stream:
stream.polygonStart();
stream.lineStart();
stream.point(0, 0);
stream.point(1, 0);
stream.point(1, 1);
stream.point(0, 1);
stream.lineEnd();
stream.polygonEnd();# stream.polygonStart()
Indicates the start of a polygon. The first line of a polygon indicates the exterior ring, and any subsequent lines indicate interior holes.
# stream.polygonEnd()
Indicates the end of a polygon.
# stream.sphere()
Indicates the sphere (the globe; the unit sphere centered at ⟨0,0,0⟩).
# d3.geoTransform(prototype)
Defines a simple transform projection, implementing projection.stream, using any methods defined on the specified prototype. Any undefined methods will use passthrough methods that propagate inputs to the output stream. For example, to invert the y-coordinates:
var flipY = d3.geoTransform({
point: function(x, y) {
this.stream.point(x, -y);
}
});Or to define an affine matrix transformation:
function matrix(a, b, c, d, tx, ty) {
return d3.geoTransform({
point: function(x, y) {
this.stream.point(a * x + b * y + tx, c * x + d * y + ty);
}
});
}# d3.geoStream(object, stream)
Streams the specified GeoJSON object to the specified projection stream. While both features and geometry objects are supported as input, the stream interface only describes the geometry, and thus additional feature properties are not visible to streams.