pm-prophet

Pymc3-based universal time series prediction and decomposition library (inspired by Facebook Prophet). However, while Faceook prophet is a well-defined model, pm-prophet allows for total flexibility in the choice of priors and thus is potentially suited for a wider class of estimation problems.

⚠️ Only supports Python 3

Table of Contents

• Installing pm-prophet
• Key features
• Differences with [Prophet]
• Peyton Manning example
• Custom Priors

Installing pm-prophet

PM-Prophet installation is straightforward using pip: pip install pmprophet

Note that the key dependency of pm-prophet is PyMc3 a library that depends on Theano.

Key Features

• Nowcasting & Forecasting
• Intercept, growth
• Regressors
• Holidays
• Additive & multiplicative seasonality
• Fitting and plotting
• Custom choice of priors (not in Facebook's prophet original model)
• Changepoints in growth
• Automatic changepoint location detection (not in Facebook's prophet original model)
• Fitting with NUTS/AVDI/Metropolis

Experimental warning ⚠️

• Note that automatic changepoint detection is experimental

Differences with Prophet:

• Saturating growth is not implemented
• Uncertainty estimation is different
• All components (including seasonality) need to be explicitly added to the model
• By design pm-prophet places a big emphasis on posteriors and uncertainty estimates, and therefore it won't use MAP for it's estimates.
• While Faceook prophet is a well-defined fixed model, pm-prophet allows for total flexibility in the choice of priors and thus is potentially suited for a wider class of estimation problems

Peyton Manning example

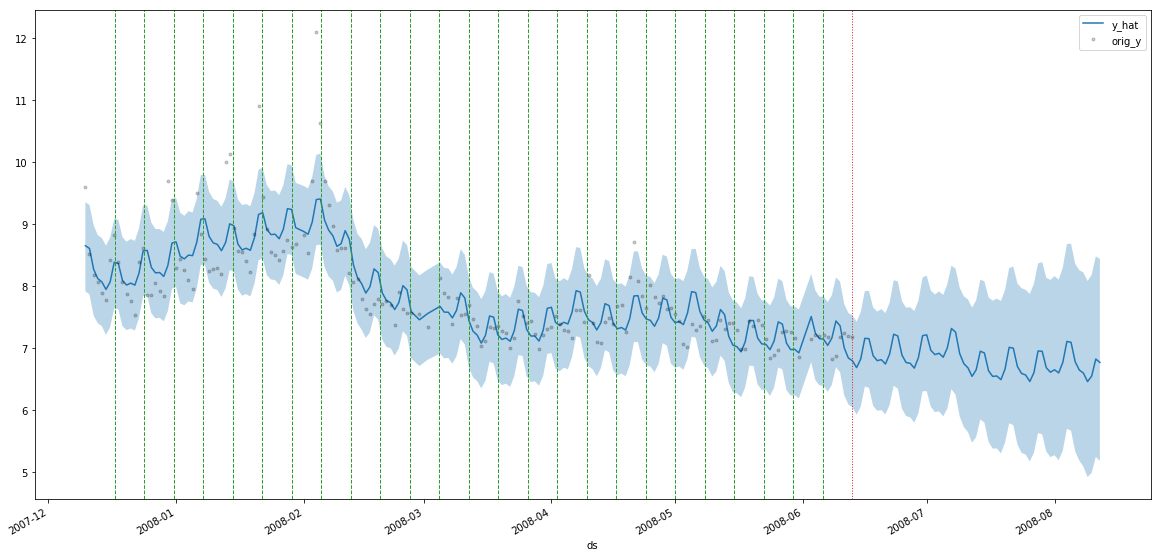
Predicting the Peyton Manning timeseries:

import pandas as pd
from pmprophet.model import PMProphet, Sampler

df = pd.read_csv("examples/example_wp_log_peyton_manning.csv")
df = df.head(180)

# Fit both growth and intercept
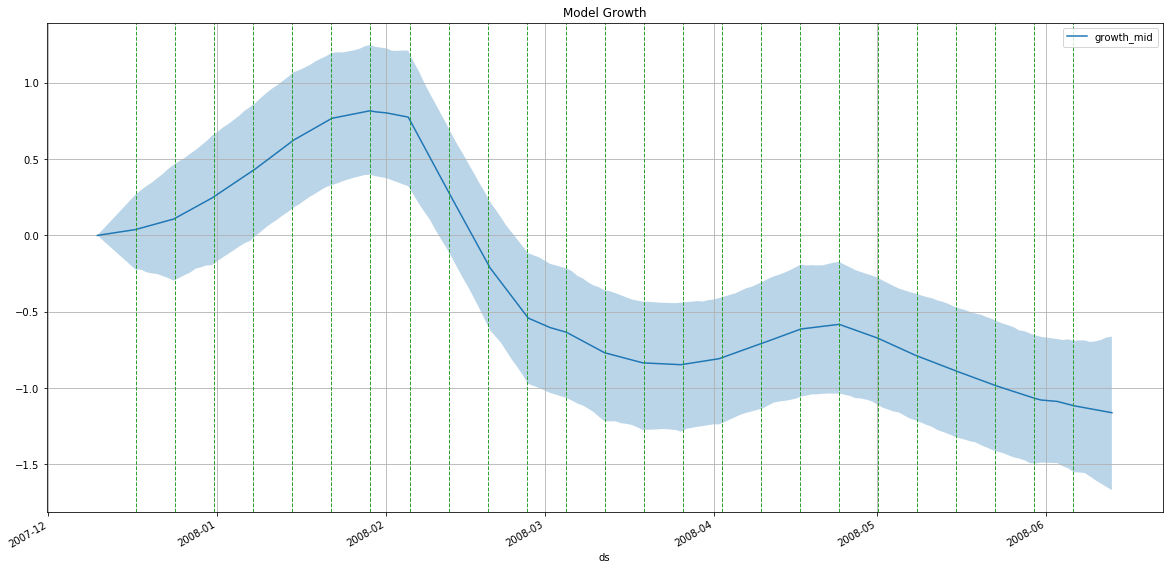
m = PMProphet(df, growth=True, intercept=True, n_changepoints=25, changepoints_prior_scale=.01, name='model')

# Add monthly seasonality (order: 3)
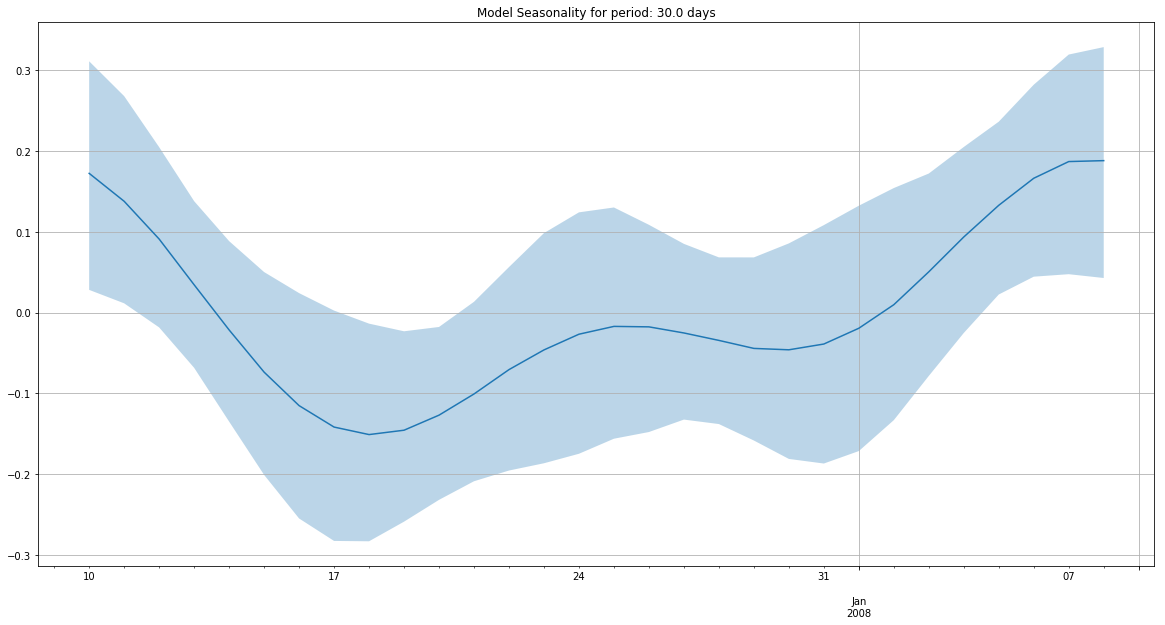
m.add_seasonality(seasonality=30, fourier_order=3)

# Add weekly seasonality (order: 3)
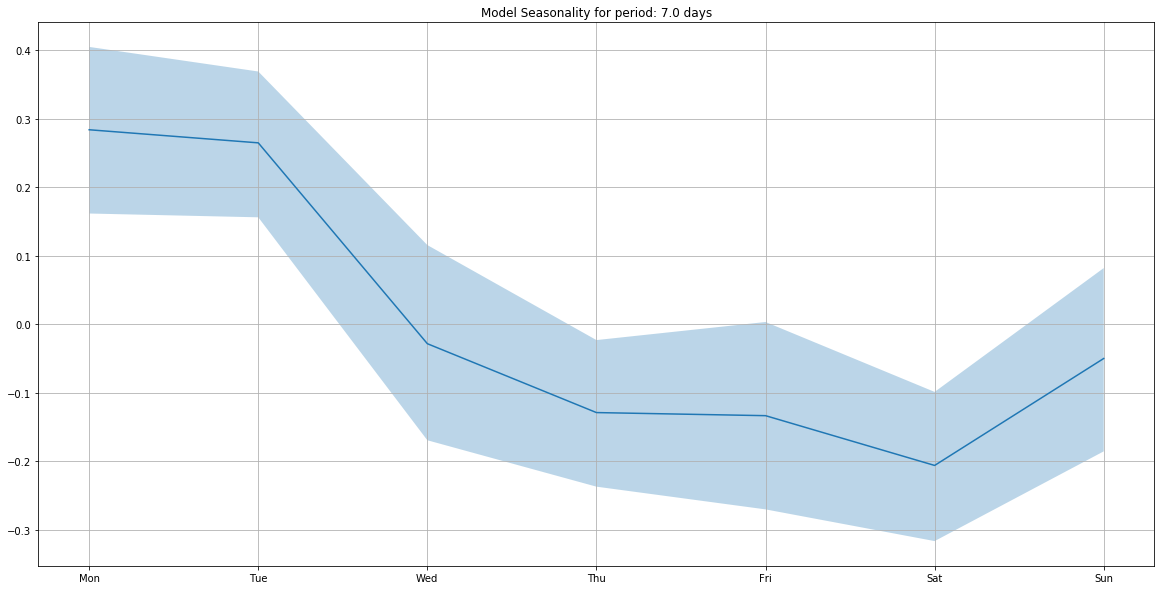
m.add_seasonality(seasonality=7, fourier_order=3)

# Fit the model (using NUTS)
m.fit(method=Sampler.NUTS)

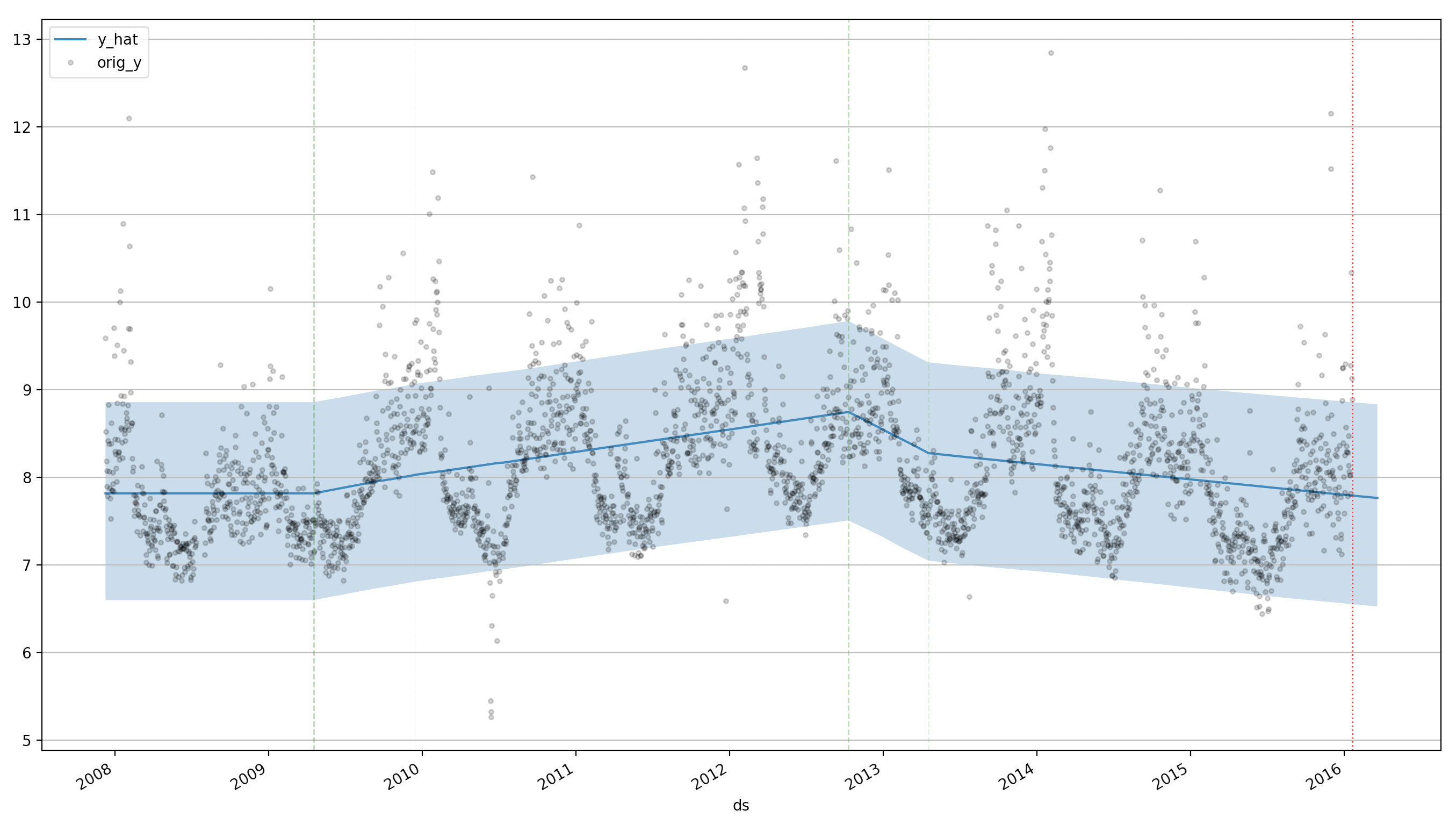
ddf = m.predict(60, alpha=0.2, include_history=True, plot=True)
m.plot_components(
    intercept=False,
)

Custom Priors

One of the main reason why PMProphet was built is to allow custom priors for the modeling.

The default priors are:

Variable	Prior	Parameters
regressors	Laplace	loc:0, scale:2.5
holidays	Laplace	loc:0, scale:2.5
seasonality	Laplace	loc:0, scale:0.05
growth	Laplace	loc:0, scale:10
changepoints	Laplace	loc:0, scale:2.5
intercept	Normal	loc:y.mean, scale: 2 * y.std
sigma	Half Cauchy	tau:10

But you can change model priors by inspecting and modifying the distributions stored in

m.priors

which is a dictionary of {prior: pymc3-distribution}.

In the example below we will model an additive time-series by imposing a "positive coefficients" constraint by using an Exponential distribution instead of a Laplacian distribution for the regressors.

import pandas as pd
import numpy as np
import pymc3 as pm
from pmprophet.model import PMProphet, Sampler

n_timesteps = 100
n_regressors = 20

regressors = np.random.normal(size=(n_timesteps, n_regressors))
coeffs = np.random.exponential(size=n_regressors) + np.random.normal(size=n_regressors)
# Note that min(coeffs) could be negative due to the white noise

regressors_names = [str(i) for i in range(n_regressors)]

df = pd.DataFrame()
df['y'] = np.dot(regressors, coeffs)
df['ds'] = pd.date_range('2017-01-01', periods=n_timesteps)
for idx, regressor in enumerate(regressors_names):
    df[regressor] = regressors[:, idx]

m = PMProphet(df, growth=False, intercept=False, n_changepoints=0, name='model')

with m.model:
    # Remember to suffix _<model-name> to the custom priors
    m.priors['regressors'] = pm.Exponential('regressors_%s' % m.name, 1, shape=n_regressors)

for regressor in regressors_names:
    m.add_regressor(regressor)

m.fit(
    draws=10 ** 4,
    method=Sampler.NUTS,
)
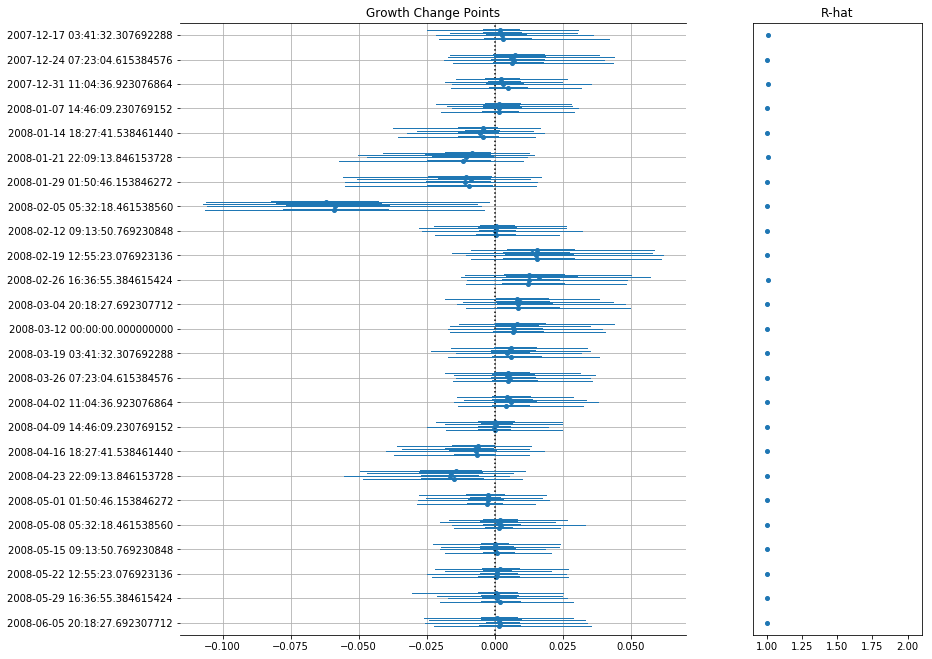
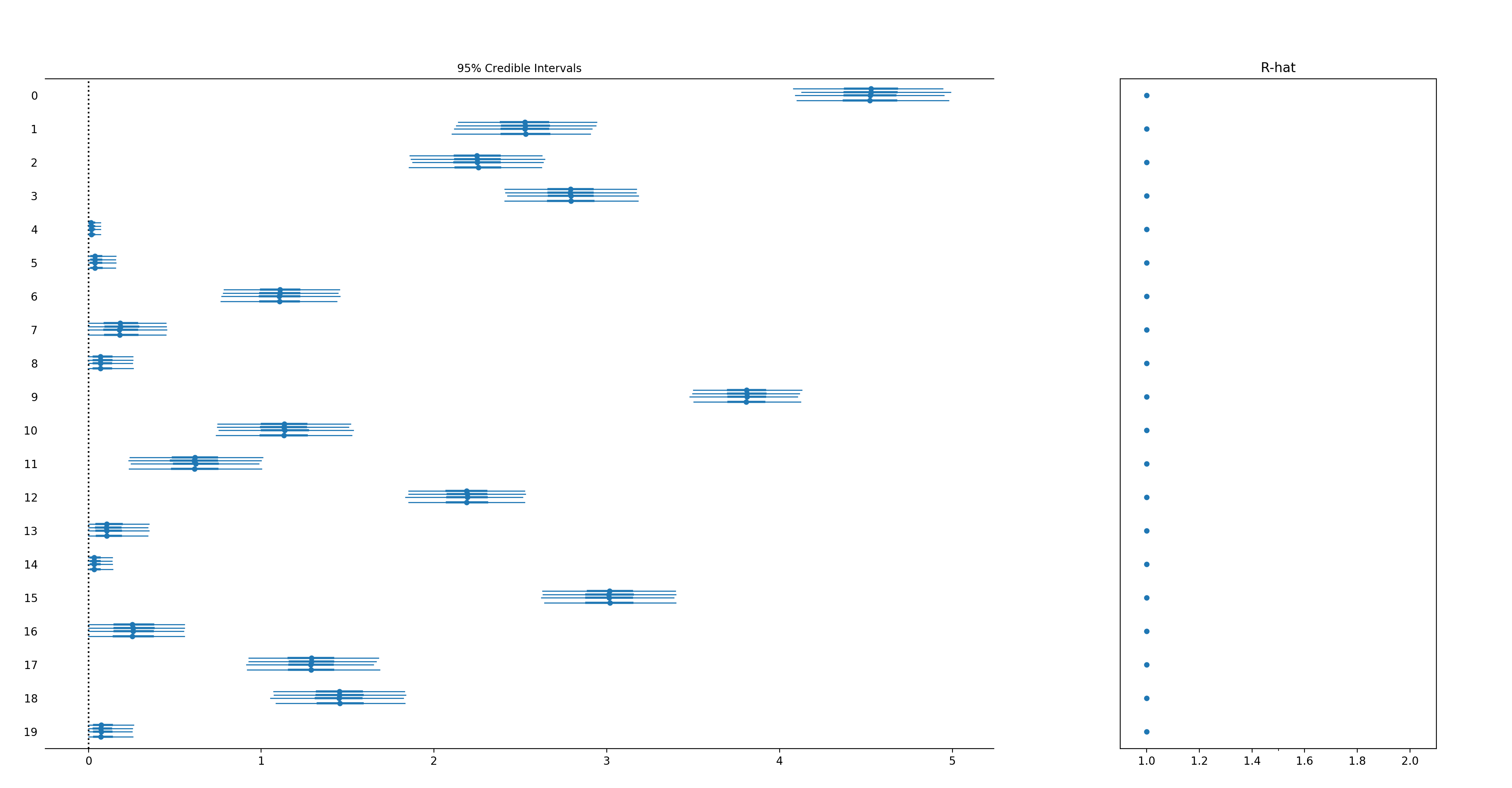
m.plot_components()

Automatic changepoint detection (⚠️experimental)

Pm-prophet is equipped with a non-parametric truncated Dirichlet Process allowing it to automatically detect changepoints in the trend.

To enable it simply initialize the model with auto_changepoints=True as follows:

from pmprophet.model import PMProphet, Sampler
import pandas as pd

df = pd.read_csv("examples/example_wp_log_peyton_manning.csv")
df = df.head(180)
m = PMProphet(df, auto_changepoints=True, growth=True, intercept=True, name='model')
m.fit(method=Sampler.METROPOLIS, draws=2000)
m.predict(60, alpha=0.2, include_history=True, plot=True)
m.plot_components(
    intercept=False,
)

Where n_changepoints is interpreted as the truncation point for the Dirichlet Process.

Pm-prophet will then decide which changepoint values make sense and add a custom weight to them. A call to plot_components() will reveal the changepoint map:

A few caveats exist:

• It's slow to fit since it's a non-parametric model
• For best results use NUTS as method
• It will likely require more than the default number of draws to converge