-
Notifications
You must be signed in to change notification settings - Fork 396
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Perspective #2
Comments
|
Took a look to the doc and If I’m not wrong there is no shadow and light parameter.. It could add a nice depth to the shapes especially if they are moving. Maybe a suggestion to explore :) |
|
Yes, this. It'd be great to have shapes change perspective in relationship to where they are on a webpage as you scroll down. |
Is it though? How would you draw a simple circle, rotated on any 3D axis? With orthographic, rotated circles are just ellipses. With perspective, you either need a polygon conversion or some way to compute a spline to fit it. ·(I’d be curious to follow the spline math if that’s what you’re thinking) |
|
The tricky thing about perspective is that the representation here is cubic Bézier segments. These are affine-invariant, which means that to apply any arbitrary affine transformation we can transform just the control points and the transformation of any arbitrary point on the curve will be correct. That is, if we call our affine transformation A, and our Bézier curve with control points [a, b, c, d] a parametric function f_[a, b, c, d] (t), we have
for every parameter value t. But perspective transformations are not in general affine. Therefore, to apply a perspective transformation we need to do more work: in general there is no exact Bézier-curve (or multi-segment Bézier spline) representation of a perspective-transformed Bézier curve, so it is necessary to approximate the perspective-transformed curve by multiple Bézier segments to within some desired level of tolerance. To implement this feature therefore requires (1) an algorithm for determining the control points of the best (or at least some) approximation of a perspective-transformed segment by a single Bézier segment, possibly under some reparametrization, (2) some kind of error metric defining the difference between two curves, (3) some scheme for subdividing the original curve, optionally optimizing the split points to reduce the number of required curves. It turns out to be just about as easy (or hard) to support applying arbitrary transformation functions as it is to just support perspective transforms. Let me recommend as one pretty performant method, https://observablehq.com/@jrus/bezplot @desandro if you want help with this feature shoot me an email or something. |
Many perspective transformations of circles are ellipses. Of course, if you go far enough you get hyperbolas instead, and then need to approximate those with cubic polynomial segments. |
|
FWIW My approach would be to add a simple scale multiply on render points given the z-distance from the origin. Definitely not mathematically accurate, but it could cover 80% of use cases in like 4 lines of code. Zdog is not trying to be the ultimate 3D engine, more like a lightweight 3D illustration tool. |



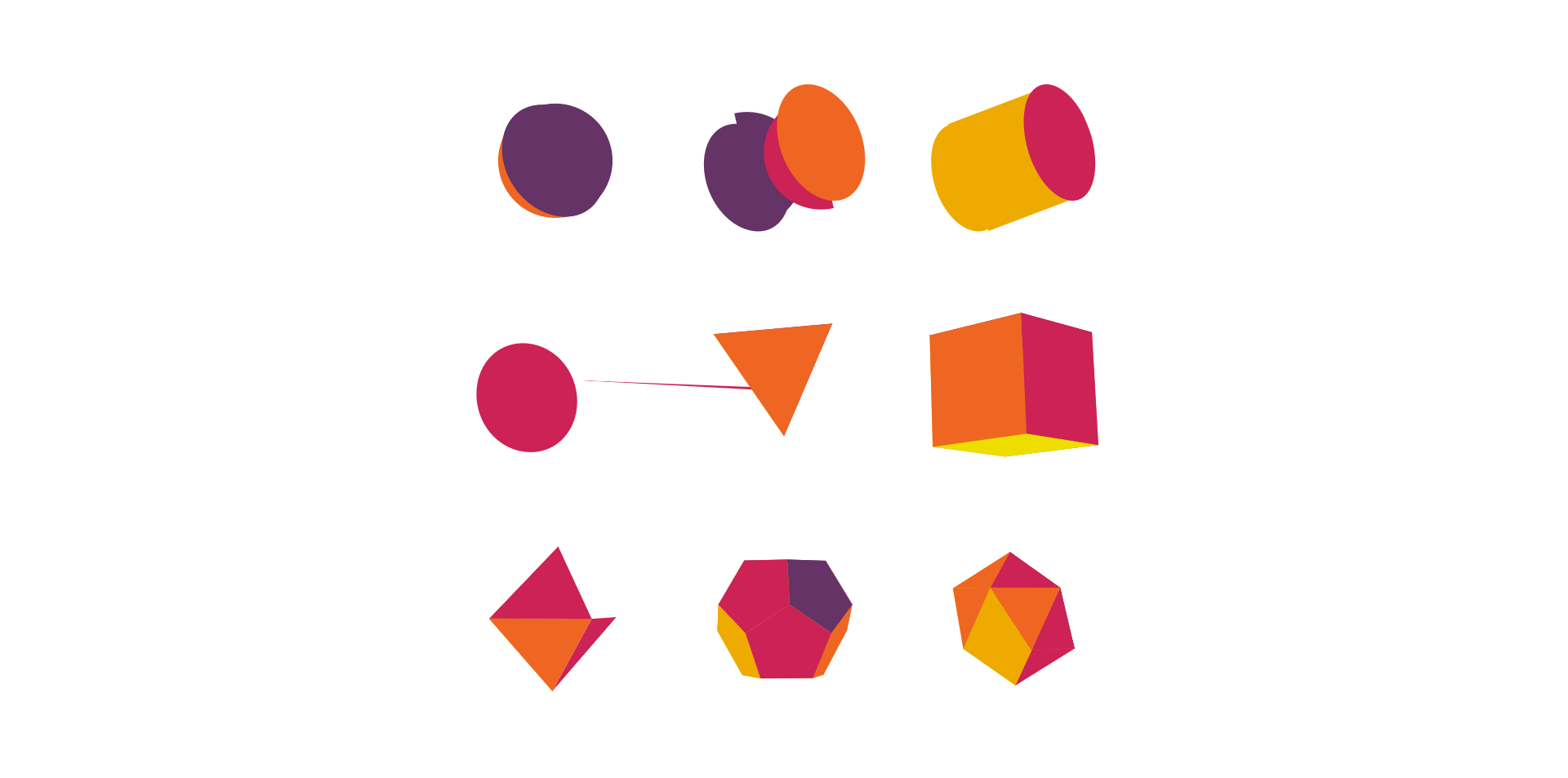

Currently Zdog uses orthogonal perspective, where all projected lines are parallel with no vanishing point. This works nice with stroke volume — as stroke volume is applied to the entire shape uniformly. So, with the same shape, a corner close to the camera will have the same stroke as the corner far from the camera.
That said, adding perspective would be a good feature to add. It's a relatively low-complexity addition that provides a wide range of capability. Vanishing point perspective is an expected feature of any 3D library. Zdog may be special, but it should get it the same.
Add a 👍 reaction to this issue if you would like to see this feature added. Do not add +1 comments — They will be deleted.
The text was updated successfully, but these errors were encountered: