This library solves an optimal transport problem via linear programming, using the Network Simplex algorithm. This code is a simplification and optimization of the Network Simplex implementation present in the LEMON 1.3.1 library. It performs much faster, uses less memory, and only requires 2 header files that can directly be integrated into your project.
If you use this code for your publications, please acknowledge LEMON and cite the paper from which this code is based:
@article{BPPH11, author = {Bonneel, Nicolas and van de Panne, Michiel and Paris, Sylvain and Heidrich, Wolfgang},
title = {{Displacement Interpolation Using Lagrangian Mass Transport}},
journal = {ACM Transactions on Graphics (SIGGRAPH ASIA 2011)},
volume = {30},
number = {6},
year = {2011},
}
The benchmark needs an OpenMP compliant C++ compiler to evaluate the multithread version performances. On linux system, just run the make command.
On MacOS with the default Apple's clang C++ compiler, install the libomp library (e.g. brew install libomp) and run the make -f Makefile.osx command.
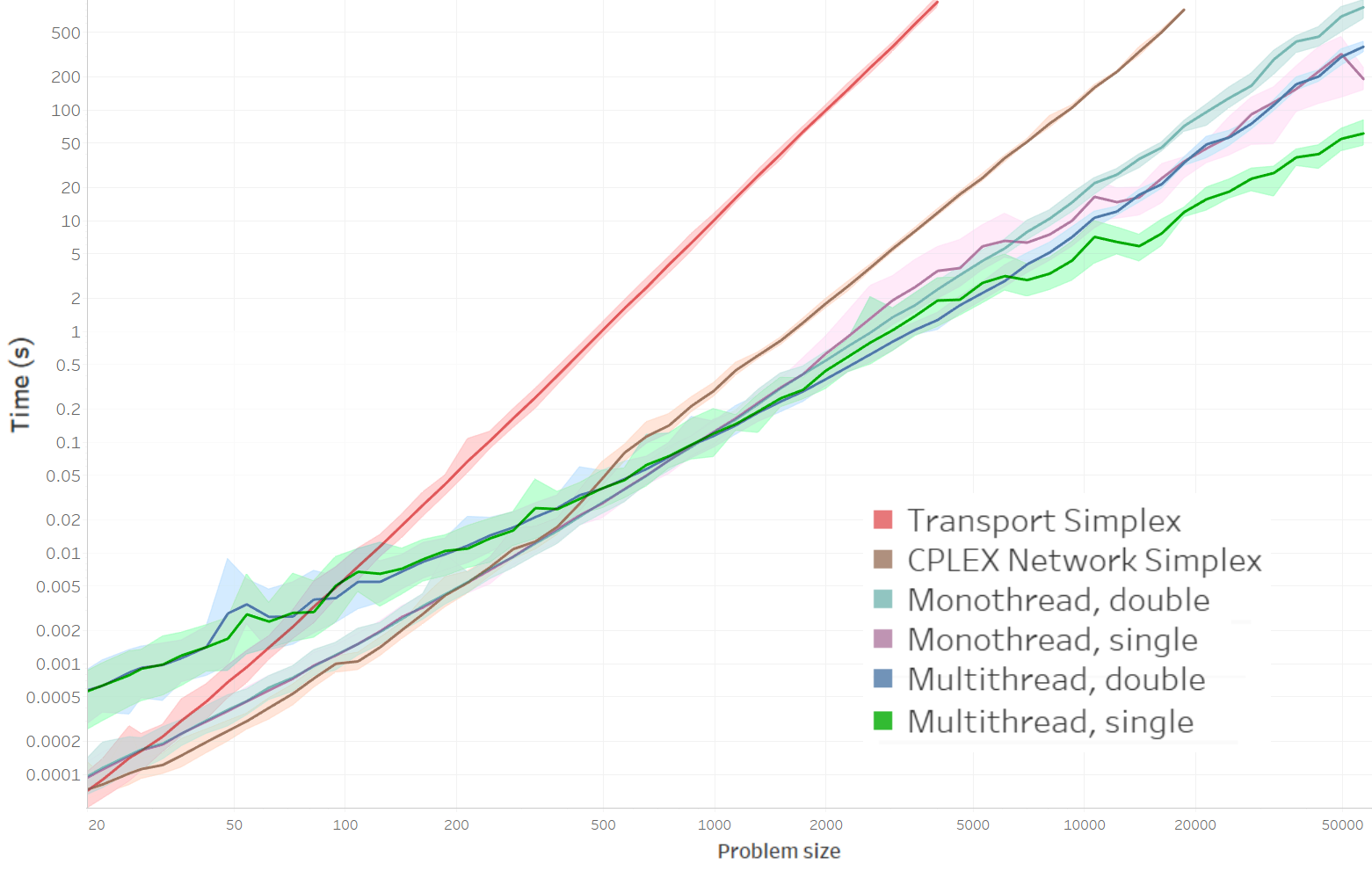
I benchmarked the code performance against CPLEX's Network Simplex (function CPXNETprimopt), and a Transport Simplex implementation (from Darren T. MacDonald).
The problem here is to compute the Earth Mover's Distance (and corresponding flow) between two histograms of N bins each (N is referred to as the problem size) using a squared Euclidean ground distance. The support of these histograms is a random sampling of the 2-D plane, and the histograms contain random values.
For the Transport Simplex, I've set the TSEPSILON to 1E-9 (the default value of 1E-6 results in largely unoptimal solutions to relatively large problems).
All values are averages over 100 runs for problems smaller than 1,000, 20 runs for problems smaller than 10,000, and 5 runs for larger problems.
- The solver allows for solving problems of size 57000 in 6min 15s on my machine on 6 physical cores in double precision, or less than 2 min for problems of size 65000 in single precision. However, single precision incur significant errors for problems of size greater than 4000 (see below).
- For problems smaller than 1000, the overhead of multithreading makes the solver slower than the monothreaded version.
- CPLEX is faster for problems smaller than 200 approximately, but becomes orders of magnitude slower for larger problems (25x slower for problems of size 19000).
- The Transport Simplex has higher complexity, and is overall slowest
- For comparison to other methods, the authors of the optimal transportation benchmark here have timed my code which runs in about 10 seconds on a single thread of their server for a problem roughly similar to their WhiteNoise example in 64x64 (though the same code runs in about 2 seconds on a laptop). This rough timing would make my code the fastest solver in their benchmark.
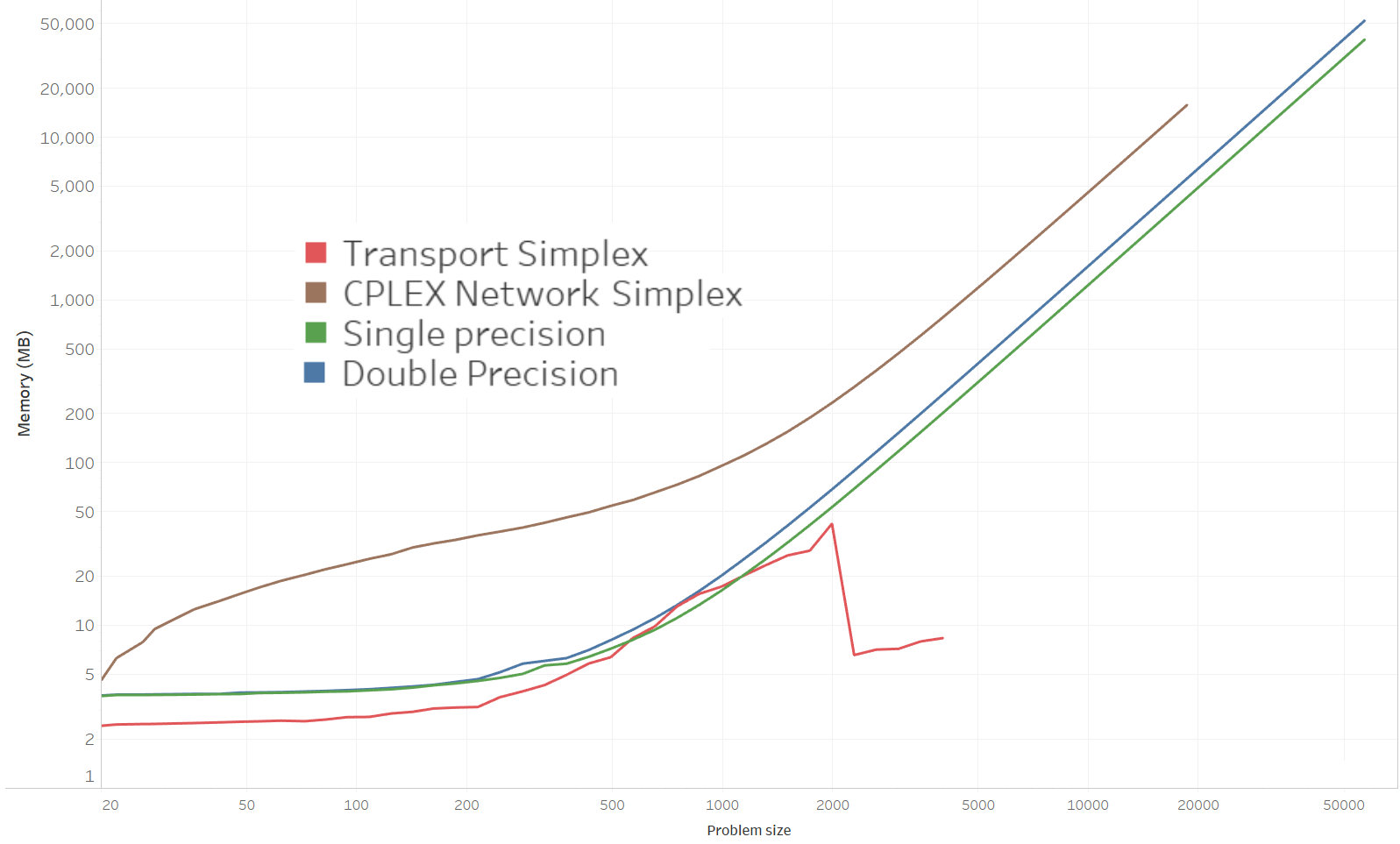
- Don't ask me what happened to the transport simplex for problems larger than 2000 (it could be an error in my memory measurement code)
- CPLEX takes more memory overall, and the Transport Simplex less.
- My code requires about 54 GB of RAM in double precision for a problem size of 57,000. Floating point precision does not halve this requirement (41 GB in practice) since much memory is required to store graph data as 32-bit integers anyway.
CPLEX is taken here as the baseline to measure the error in Earth Mover's Distance.
- On the 3355 runs of various sizes in total, my code gave (epsilon) better EMD than CPLEX 2393 times, and (epsilon) worse than CPLEX 920 times, though when the EMD is worse, it's significantly more than when it's better (though still negligible for most applications). It gave the exact same result 42 times (to 24 digits).
- The graph above shows percentages. For large problems of about 25,000 bins, my code results in EMD less than 0.001% higher than CPLEX. For problems larger than 25,000 bins, CPLEX does not terminate (it ran 6 hours for a problem of about 28,000 bins).
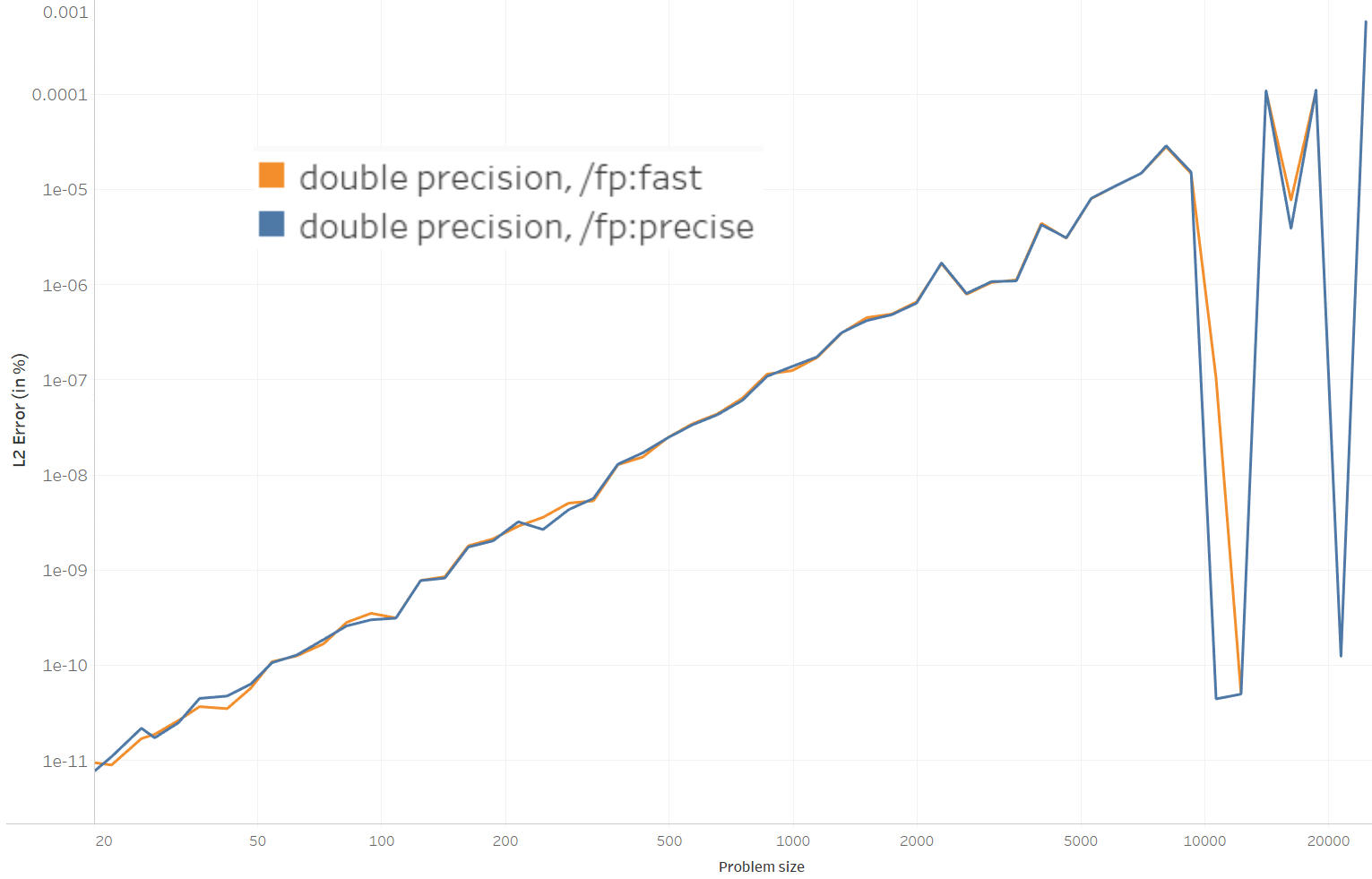
- Compiling with the floating point precision modes fp:fast (which favors fast code) or fp:precise (for more precise computations) in Visual Studio does not change the result much.
- The noise at the end of the curve is just due to less runs being averaged (5 instead of 20 or 100).
I am not sure how relevant it is to compare the EMD computed with values in single precision to the EMD computed with values in double precision. Here is the graph anyway.
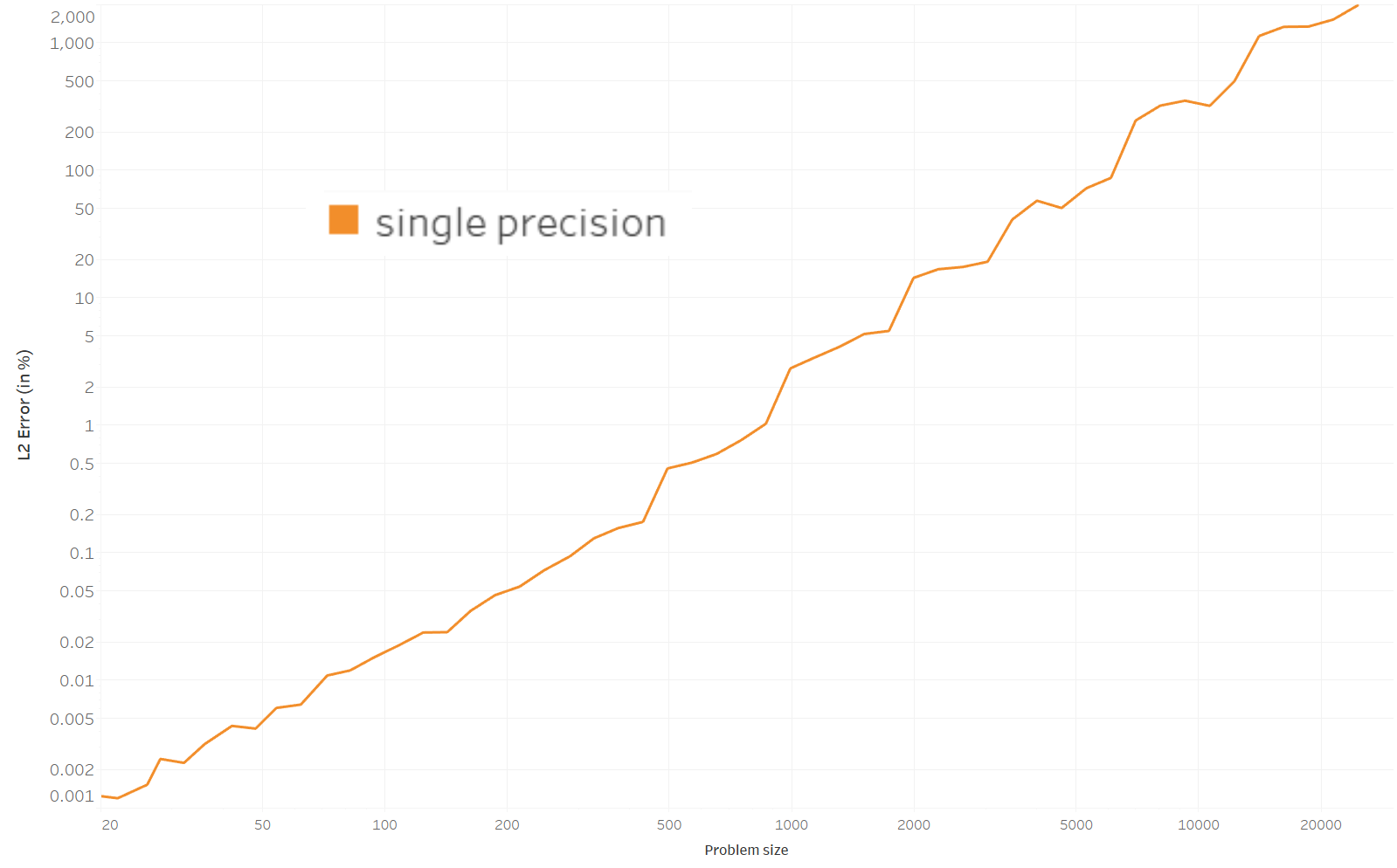
- The error rapidly grows to reach 2000% for a problem size of 25,000. The error remains reasonable (<15%) for problems smaller than 2000.
- I only computed the error in term of EMD, but other metrics could be more relevant here, especially on the transport plan itself.
- However, the visual impact of even large errors seems moderate. Below is an animation of Monge<->Kantorovich, in the special case of the assignment problem, both computed in double and single precision. There are visible differences, though not completely obvious: the speed of particles is mostly more homogeneous / coherent in double precision.
| Double precision | Single precision |
|---|---|
 |
 |
This has been computed in 577 seconds in double precision with 55,000 points, and 516 seconds in single precision.
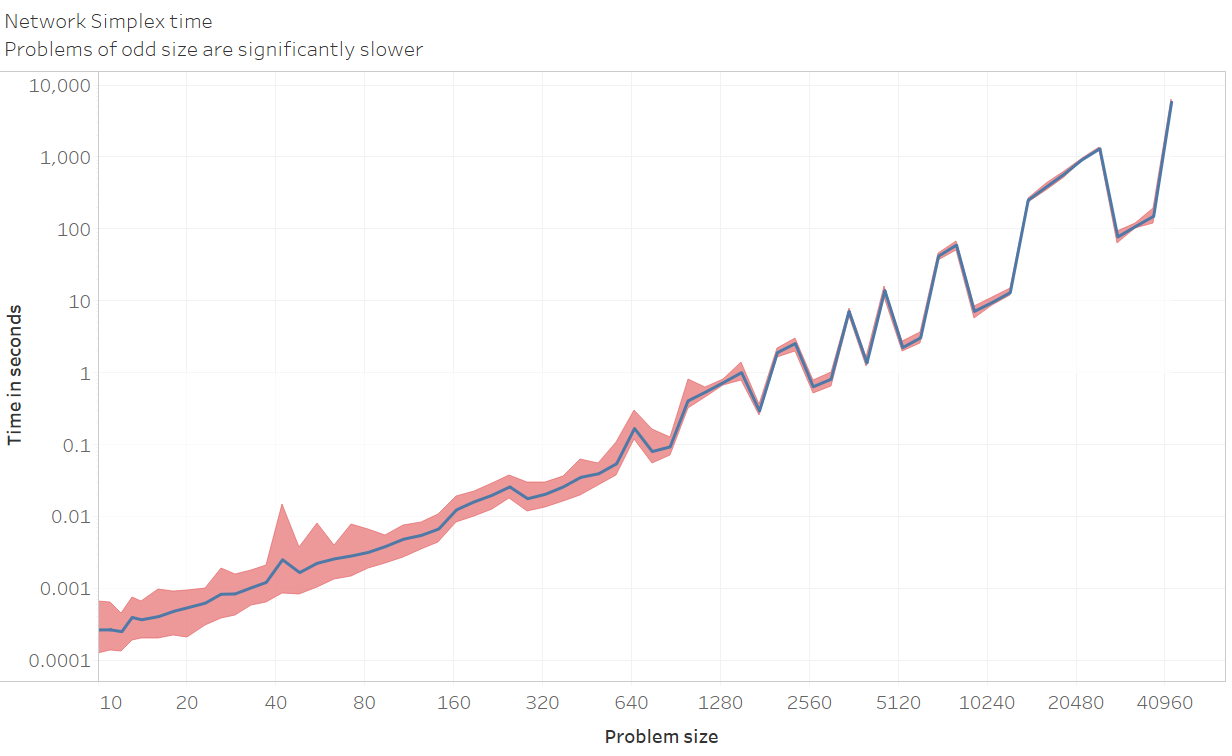
- My code becomes orders of magnitude slower on problems of odd sizes. The speed graph above is restricted to problems of even sizes, and a graph that includes some odd sizes problems can be found below:
If you absolutely need to solve a large odd sized problem, it could be a good idea to add a ghost supply and demand with infinite cost to all other nodes, and 0 cost between the ghost supply and ghost demand.