The Algorithm stood second fastest in the organized Inter-University competition(year 2017) in Osaka, and needs no extra storage space/buffers. Second fastest only to a Randomized Dynamic programming algorithm, which has a small chance of giving an invalid answer.
Problem Statement : From a set of N numbers from 1 to 1,000,000, find a subset that sums up to a random number X (1,000,000 < X < N×1,000,000). In theory, this is an NP-Complete Problem, however, we aim to solve this in linear time WITHOUT using dynamic programming and the large memory usage associated with it.
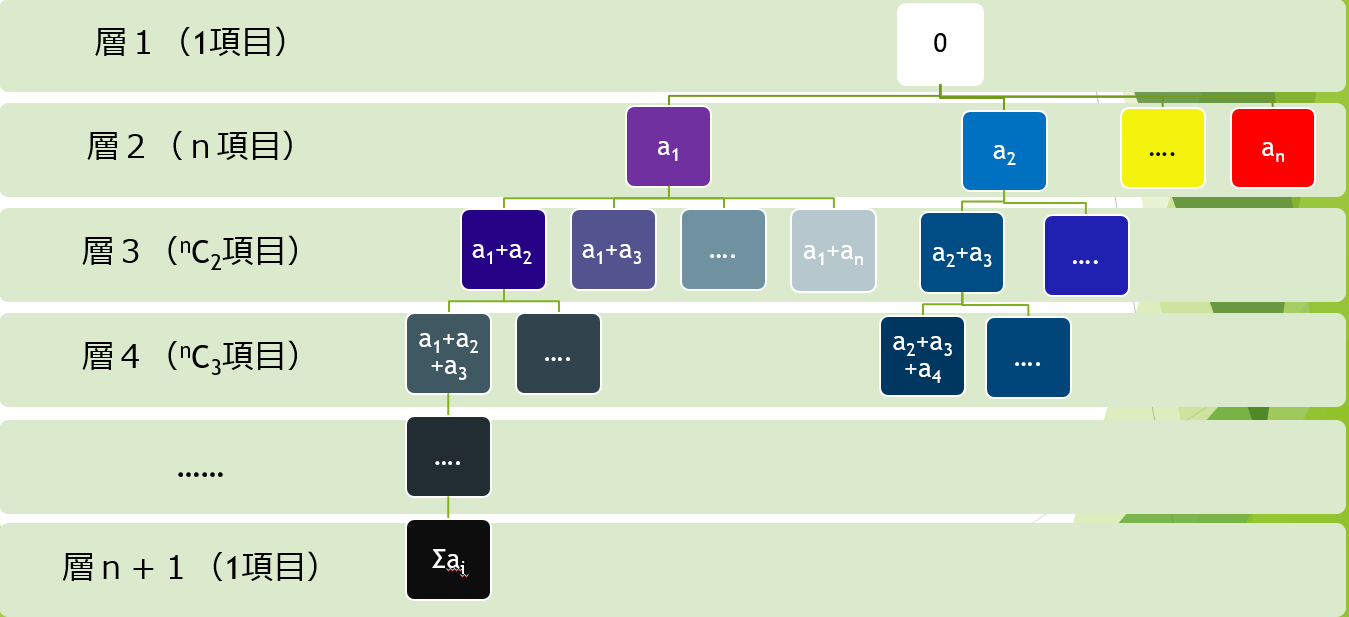
Algorithm : We think of the N numbers sorted in descending order as a1,a2,a3,....an. Hence, a1>a2...>an. Then, we do a Depth First Search on the following tree, trying to match the sum of the a's with 'X'. The DFS is then optimized using the mathematical inequality of a1>a2...>an.
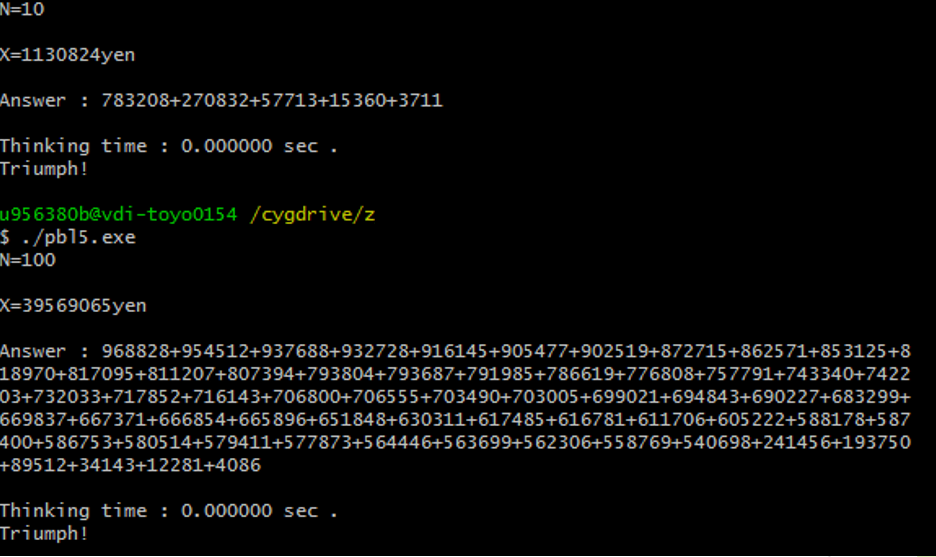
An Example run is as below, Number of terms to find N=10 and 100, takes zero time.
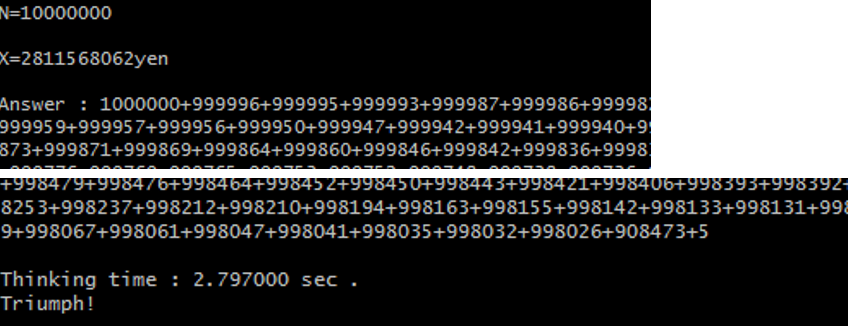
Number of terms to find N=10,000,000?? Now that's something! Takes under 3 seconds :
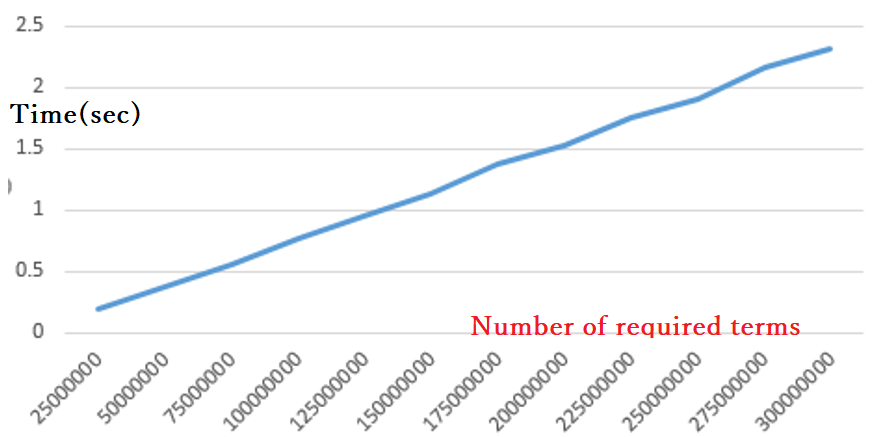
The graph of time taken vs number of terms N was linear, as below: