LFSR ON FPGA

• 封面

[TOC] 开源地址

图片加载不出来？点这里查看pdf

---

1.迭代日志

项目开发中，待完善......

• 2021/09/02 modify log:

  1. galois型lfsr开发与仿真：只支持3~16bit，代码不规范，通用性不强，仿真用例简单。

• 2023/03/19 modify log:

  1. fibonacci型lfsr开发与仿真：支持3-->168bit；

  2. galois型lfsr更新到V2.0版本：支持bit数更新为3-->20,32,64,128bit；

• 2023/04/08 modify log:

  1. 完成matlab代码（用于生成抽头矩阵verilog代码）；
  2. 完成所有模块代码更新；
  3. 修改仿真do脚本文件，优化文件管理结构；

• 2023/04/09 modify log:

  1. 完成部分markdown文档编写；

• 2023/04/10 modify log:

  1. 修复fabonacci模块的一个语法bug；
  2. 添加lsfr.xmind文件；
  3. 更新markdown，同步更新pdf；

• 2023/04/11 modify log:

  1. 增加xilinx FPGA工程，并使用tcl脚本加入git管理；

• 2023/04/12 modify log:

  1. 更新相关文档和图片；

---

2.项目简介

• 本项目是一个用于FPGA平台的LFSR模块代码；
• 使用Verilog HDL语言进行开发；
• 主要目的是为了方便FPGA工程师做接口的数据校验工作，如SERDES、DDR、JESD、SRIO等高速接口，还有以太网、UART、SPI、IIC等接口的通信链路(读写/收发)测试；
• 用winsows批处理加do文件脚本在Modelsim上进行仿真验证（独立仿真）；
• 参考了Xilinx的xapp052.pdf文件中提供的高达168bit的本原多项式抽头；
• 包含Galois和Fibonacci两种类型LFSR的实现；
• 使用matlab辅助进行verilog开发；
• 方便版本控制的文件管理结构；

---

3.原理介绍

• 什么是LFSR？

  维基百科LFSR

  LFSR即Linear-feedback shift register，线性反馈移位寄存器，就是一种带反馈的移位寄存器，通过抽头系数进行反馈，使得移位寄存器的输出符合某种规律；

  根据反馈抽头方法的不同，包括以下两种构型：

  Galois型（one-to-many）：

  

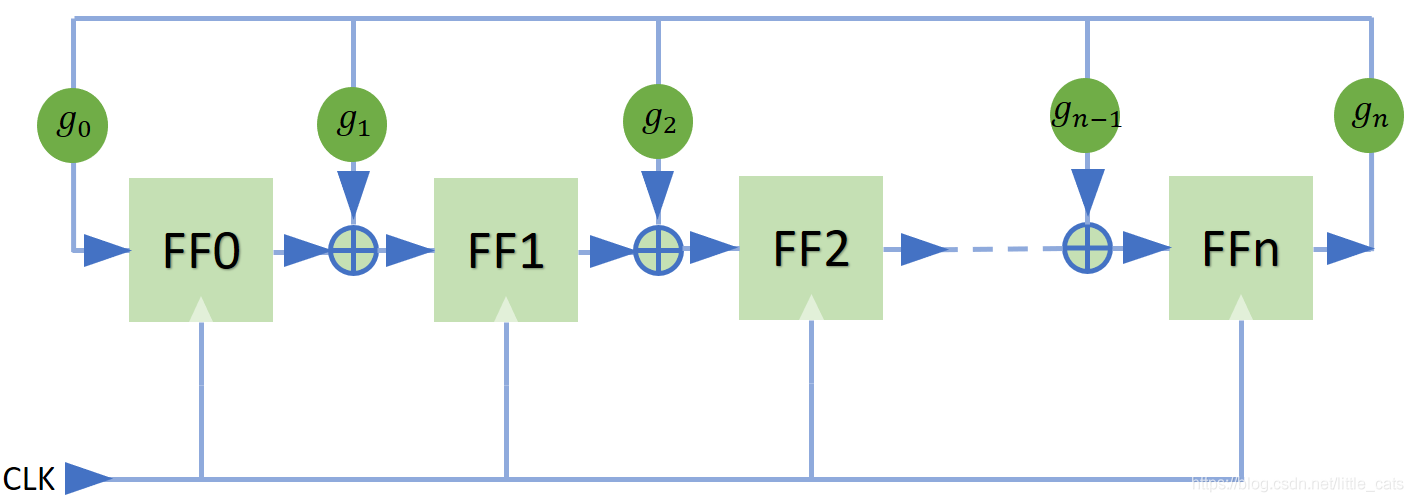
  Galois型又叫one-to-many型，从图中可以看出，每一触发器的D端是前一触发器的Q端和抽头结果异或（同或）的结果，抽头系数g的取值只有0和1两种结果，即抽头或者不抽头，抽头的位置是同一个位置，即最高位（最低位）；从同一个位置（one）抽头，反馈到不同寄存器的D端（many），所以叫他ont-to-many。

  Fabonacci型(many-to-one)：

  

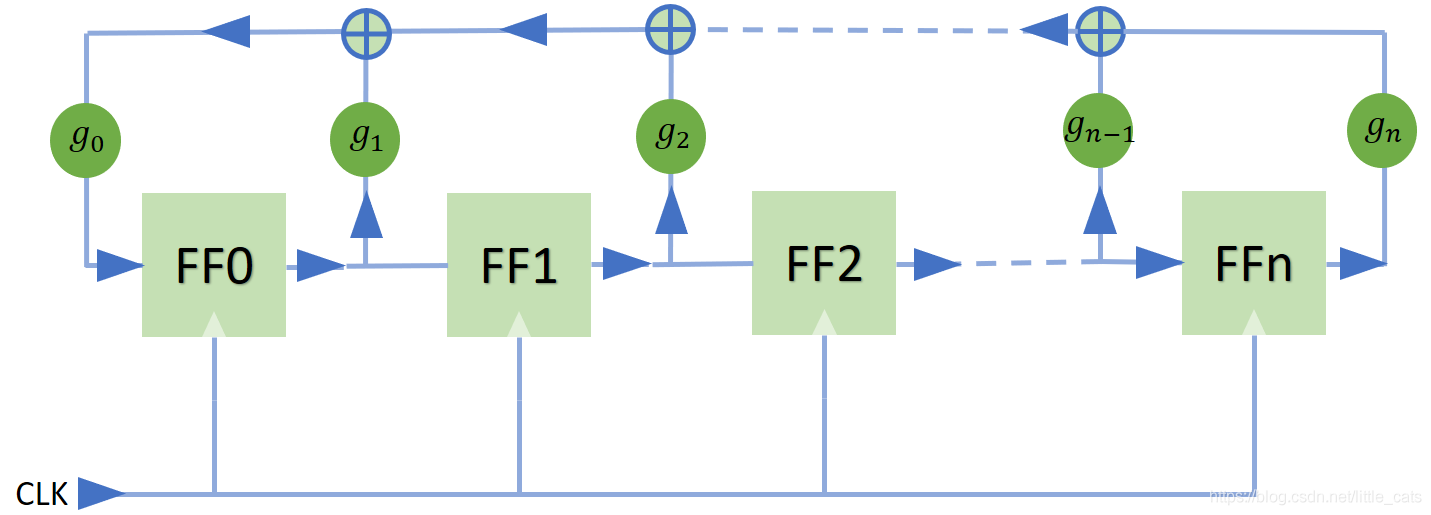
  Fabonacci型又叫many-to-one型，从图中可以看出，所有的抽头的异或（many）反馈到同一个触发器的D端，，所以叫他ont-to-many。

• 数学表达

  $$ R(x) = \frac{M(x)} {G(x)} $$

  其中，R(x)是输出多项式，M(x)是输入多项式，G(x)是特征多项式（生成多项式）。 对于一个N位的寄存器，最多有2^N个不同的状态，但是由于全0（或全1）会导致移位寄存器陷入死循环，所以N位LSFR能产生的最长不重复序列的个数为： $$ 2 ^ N - 1 $$

  此最长不重复序列称为最长输出序列，N位的LFSR，可用的抽头至少有n个（第0个抽头是必须的，不算），所以可以有很多种不同的抽头配置，但不是所有抽头都能使其达到最长输出序列，能使输出R(x)成为最长输出序列的特征多项式称为本原多项式。

  值得注意的是，本原多项式并非只有一个。

  如N为3时，本原多项式可以是：

  $$ X ^ 3 + X ^ 2 + 1 $$

  或

  $$ X ^ 3 + X ^ 1 + 1 $$

• LFSR的应用

  • PRBS发生器；
  • 白噪声发生器；
  • CRC计算；
  • ......

• 代码实现

  1. Galois：

     integer i;
     always@(posedge clk  or posedge rst) begin
         if(rst) begin
             x_lfsr <= DEFAULT_SEED;
         end else begin
             if (enable) begin
                 if(load_evt) begin
                     x_lfsr <= seed_data;
                 end else if(~lfsr_vld & ~seed_load_flag) begin
                     x_lfsr <= DEFAULT_SEED;
                 end else begin
                     x_lfsr[1] <= x_lfsr[BIT_WIDTH] ^ fb_vec[0];
                     for (i=2;i<=BIT_WIDTH;i=i+1) begin: x_lfsr_gen
                         x_lfsr[i] <= x_lfsr[i-1] ^ fb_vec[i-1]; 
                     end 
                 end
             end
         end
     end

     根据逻辑代数公式： $$ A \oplus 0 = A\ $$ 所以，只需对fb_vec进行迭代，抽头时fb_vec[i] = x_lfsr[BIT_WIDTH]，不抽头时fb_vec[i] = 0；

  2. Fabonacci:

     always @(posedge clk or posedge rst) begin
         if (rst) begin
             r_lfsr <= DEFAULT_SEED; 
         end else begin
             if (enable) begin
                 if (load_evt == 1'b1) begin
                     r_lfsr <= seed_data;
                 end else if (~lfsr_vld & ~seed_load_flag) begin
                     r_lfsr <= DEFAULT_SEED;
                 end else begin
                     r_lfsr <= {r_lfsr[BIT_WIDTH-1:1], r_xnor}; 
                 end
             end
         end 
     end

  3. 种子的选择

     不难注意到，上述两段代码中分别使用了异或和同或对LFSR进行实现，那么两者有何不同呢？

     运算逻辑的选择跟种子序列状态有关，由于

     $$ 0 \oplus 0 = 0 \ 1 \odot 1 = 1 $$

     所以用异或实现的LSFR不能出现全0状态，用同或实现的LFSR不能出现全1状态，基于此考虑，两种LFSR的默认种子均设置为**“0...001”**，确保不会陷入死循环。

  4. 完整代码实现请看源文件

---

4.详细设计

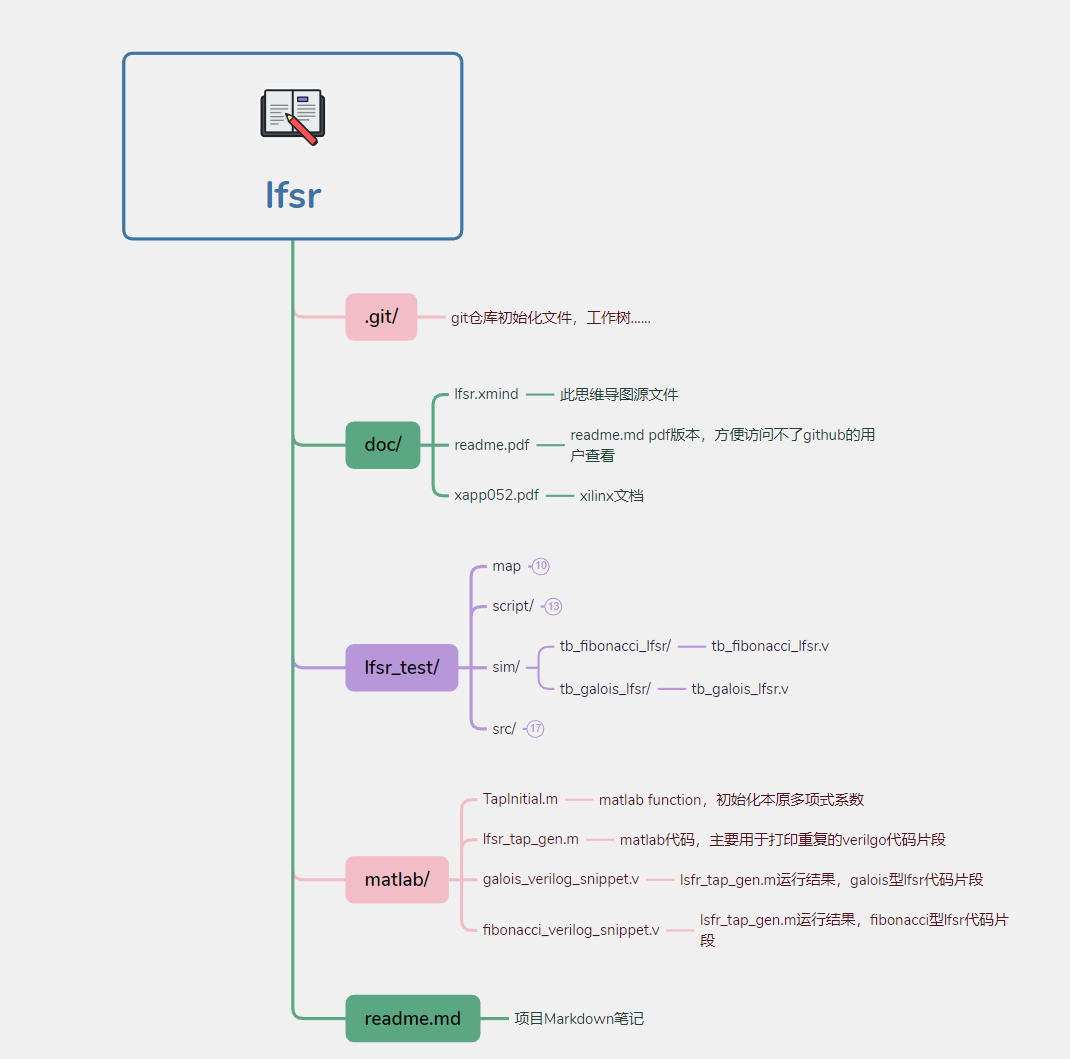
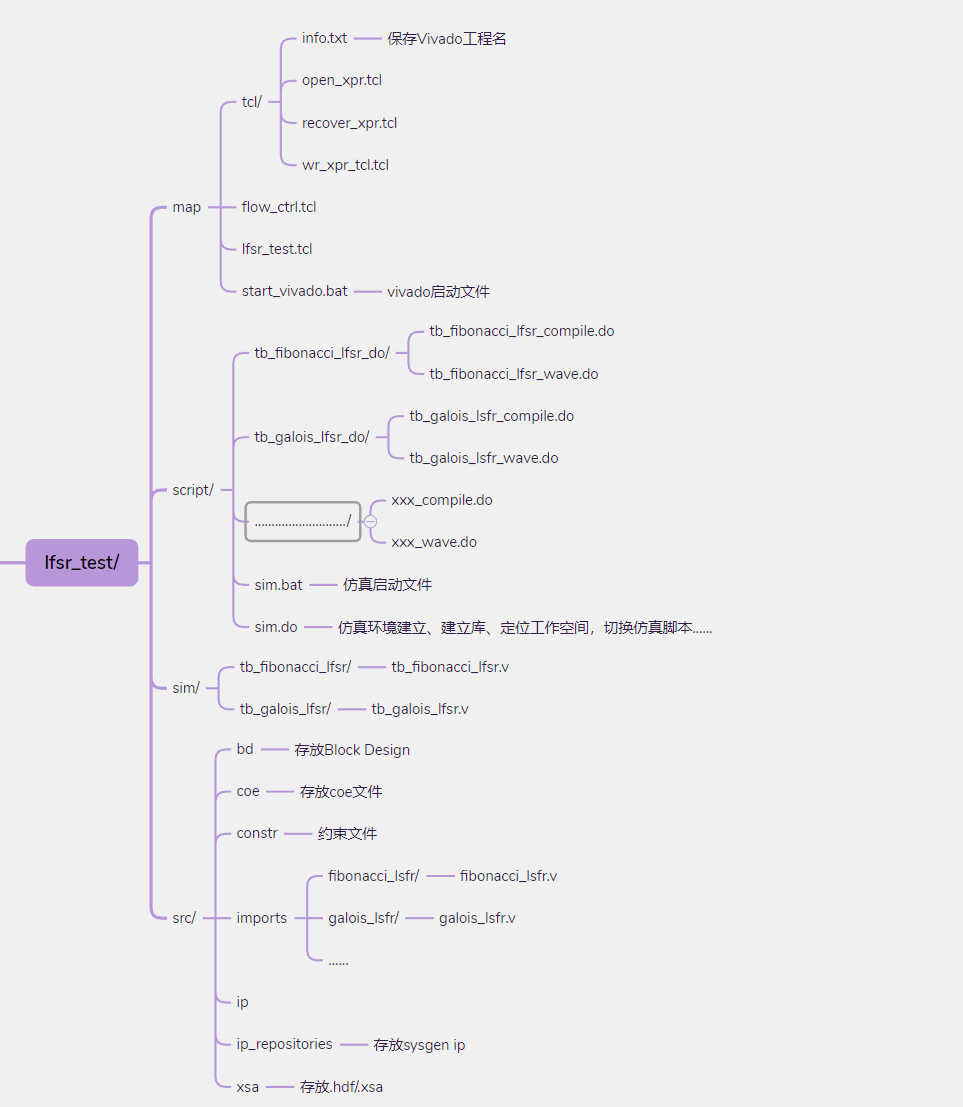
• 文件管理结构说明

  下图为此项目文档结构，按照这种方式进行管理主要出于以下考虑：

  • 方便git进行管理；
  • 不影响modelsim仿真；
  • 不影响在此基础上建立FPGA工程；

  注意事项：

  当你运行一次仿真之后，./lfsr_test/script路径下会出现一些modelsim仿真产生的文件（编译结果，仿真库、波形文件等等），这些文件只是临时文件，仿真完成后可直接删除，并不影响项目的文件管理结构，因此也并没有加入到git版本控制当中。

  项目文件结构：

  

  FPGA工程文件结构：

  

​

• 运行项目

  1. 运行前提，电脑已安装modelsim软件，并且设置好了环境变量；

     测试方法，在windows命令行中运行

     vsim

     如果modelsim能够启动，则说明环境已准备好；

  2. 双击lfsr_test/script路径下的sim.bat文件，即可运行仿真；

  3. 切换不同模块的仿真；

     下面是sim.do文件的代码：

     quit -sim  
     .main clear
     
     # shift to upper level direction
     cd .. 
     
     set BASE_HOME [pwd]
     
     set DO_HOME  $BASE_HOME/script/ 
     set SRC_HOME $BASE_HOME/src/ 
     set SIM_HOME $BASE_HOME/sim/ 
     
     cd $DO_HOME 
     
     vlib ./work
     vlib ./work/modelsim_lib
     
     vmap work ./work/modelsim_lib
     
     do {./tb_galois_lfsr_do/tb_galois_lfsr_compile.do}
     # do {./tb_fibonacci_lfsr_do/tb_fibonacci_lfsr_compile.do}

     注意最后两行，当前是对galois_lfsr进行仿真，如果想要仿真fibonacci_lsfr，只需将最后两行代码改成

     # do {./tb_galois_lfsr_do/tb_galois_lfsr_compile.do}
     do {./tb_fibonacci_lfsr_do/tb_fibonacci_lfsr_compile.do}

  4. 仿真结果查看；

     看波形中lfsr_done是否为周期性单脉冲，周期为： $$ 2 ^ N - 1 $$

• 注意事项

  本人只对24bit以下的两种LFSR进行了仿真，24bit以上时，由于仿真所需时间太长，并没有进行仿真，在你直接使用之前，最好进行充分仿真测试，即使仿真时间太长，也应该核对一下所使用的阶数对应的抽头多项式是否正确。

  核对方法：比较doc/xapp052.pdf中与matlab/TapInitial.m代码中对应的抽头系数是否一致。

---

5.开发者说

• 想法

  整个项目设计过程中最麻烦的事情就在于根据本原多项式的抽头系数写出抽头矩阵，由于不同bit之间的抽头系数完全没有规律，所以只能一个个进行人工录入，考虑到Fabonacci和Galois的构型不同，代码的写法也不同，如果按部就班，意味着这种无聊至极的事情要做两遍，这让人非常崩溃，所以笔者选择写个matlab代码，只写一遍抽头系数，然后把两种构型的verilog代码片段打印出来。但是，在matlab中仍然要进行一次录入，那么问题来了，能不能写个算法，可以根据bit数自动计算出本原多项式（系数），尽管不同阶数的本原多项式不止一个，但我们只需要任意一个就ok了！！！

  这个项目并不复杂，这些做法也并不是完全有必要，但是通过这个项目的开发，也使我思考，如何使用不同的语言、环境来对FPGA工程师的开发进度进行加速呢？

• 声明

  • 封面的水墨图片来源于网络，时间太久不记得出处了，有任何版权上的问题请联系我；

  • 原理介绍中的两张图片来源于一篇博客；

  • galois模块代码最初版本参考了网上的一份代码，已在代码注释中标出；