pyxu_xrt provides Pyxu operators to compute samples of the X-Ray Transform in 2D and 3D.
The X-Ray Transform (XRT) of a function f: \mathbb{R}^{D} \to \mathbb{R} is defined as
\mathcal{P}[f](\mathbf{n}, \mathbf{t})
=
\int_{\mathbb{R}} f(\mathbf{t} + \mathbf{n} \alpha) d\alpha,
where \mathbf{n}\in \mathbb{S}^{D-1} and \mathbf{t} \in \mathbf{n}^{\perp}. \mathcal{P}[f] hence denotes the set of line integrals of f.
Two class of algorithms exist to evaluate the XRT:
- Fourier methods leverage the Fourier Slice Theorem (FST) to efficiently evaluate the XRT when multiple values of \mathbf{t} are desired for each \mathbf{n}.
- Ray methods compute estimates of the XRT via quadrature rules by assuming f is piecewise constant on short intervals.
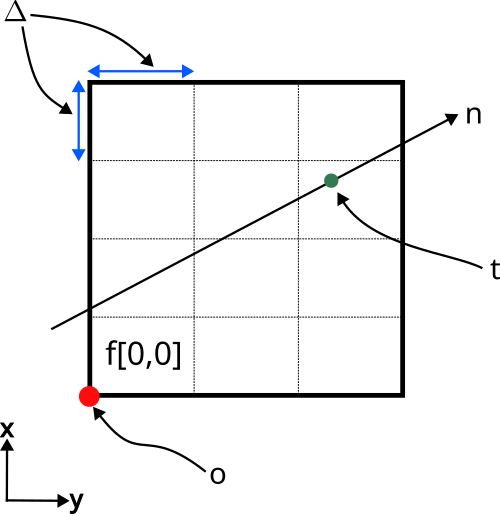
The operators in pyxu_xrt allow one to efficiently evaluate samples of the XRT assuming f is a pixelized
image/volume where:
- the lower-left element of f is located at \mathbf{o} \in \mathbb{R}^{D},
- pixel dimensions are \mathbf{\Delta} \in \mathbb{R}_{+}^{D}, i.e.
f(\mathbf{r}) = \sum_{\{\mathbf{q}\} \subset \mathbb{N}^{D}}
\alpha_{\mathbf{q}}
1_{[\mathbf{0}, \mathbf{\Delta}]}(\mathbf{r} - \mathbf{q} \odot \mathbf{\Delta} - \mathbf{o}),
\quad
\alpha_{\mathbf{q}} \in \mathbb{R}.
In the 2D case, the parametrization is best explained by the figure below:
You can install pyxu_xrt via pip:
pip install pyxu_xrtThe host system must have CUDA 11.x or 12.x installed to use the GPU. Similarly, using drjit-backed operators on the CPU requires LLVM. If problems arise, we provide Docker receipes to easily create Pyxu developer environments.
Distributed under the terms of the MIT license, pyxu_xrt is free and open source software.
If you encounter any problems, please file an issue along with a detailed description.