Computer Vision and Image Processing
Wavelet Edge Detection
CSE 573 - Fall 2015
In this project, we have to design a wavelet transform based scheme for edge detection. In particular, the wavelet transforms at two adjacent scales are multiplied in order to magnify edge structure and suppress noise. The following steps are to be performed:
(a) Select from several possible wavelet transforms and determine which two to use with convincing reasons
(b) Add Gaussian noise and impulse noise, respectively, to the test images for your implementation; You may select the level of noise with explanation in your report
(c) Perform the selected wavelet transforms to at least three different test images and their noise corrupted versions; The transform should be performed for at least four levels
(d) Perform proper scale multiplications to each of the wavelet transformed images and combine the results at different levels to form the final edge map
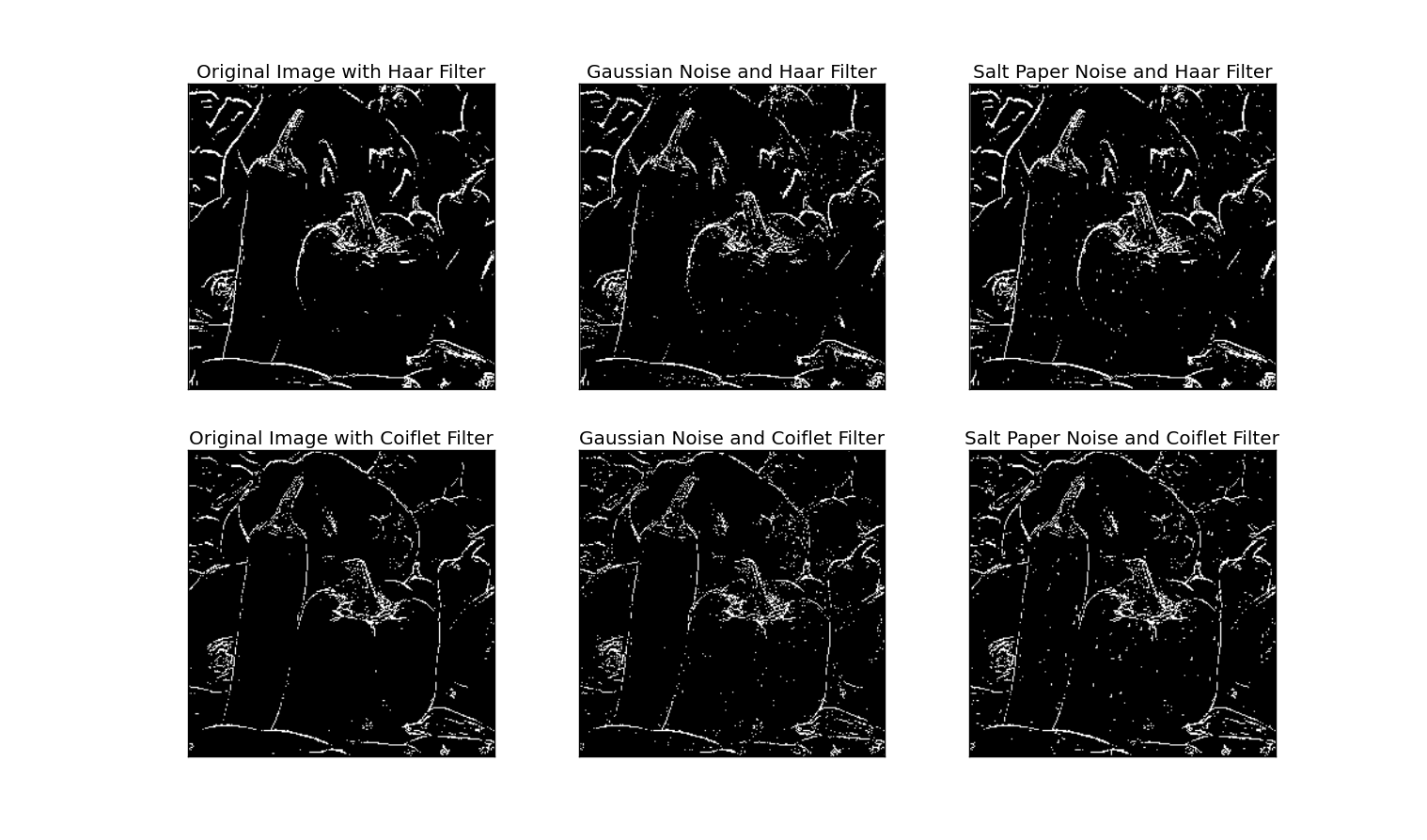
(e) Display the test images and their final edge detection results based on two different wavelet transforms.
(f) Compare the results of edge detection from two different wavelet transforms and from two different noise types; Explain the difference among these results
(g) Bonus (5%): Implement an edge detection scheme combining wavelet
Edge detection is a very prevalent problem in the field of image processing and has been researched a lot. Some edge detection techniques fall in the spatial domain edge detection like Canny and sobel. The other category is edge detection in the frequency domain.
Mallat and Zhong in their work[1] proposed a dyadic wavelet and a corresponding wavelet transform. The idea was to detect edges in the wavelet domain by applying wavelet transform to the image in different scales. It was observed that the edge structures were visible in each sub-band but the noise levels decreased rapidly along these scales.
Xu et al[2] presented a method in which they enhanced significant structures by multiplying the adjacent DWT levels and Sadler and Swami[3] analyzed the multi-scale product in step detection and estimation . The paper[4] we are following does something along these lines; we make a multi-scale edge detector by multiplying adjacent sub-bands and making edge maps at different scales and combining them in the end. Edges are determined as local maxima in the product function after thresholding.
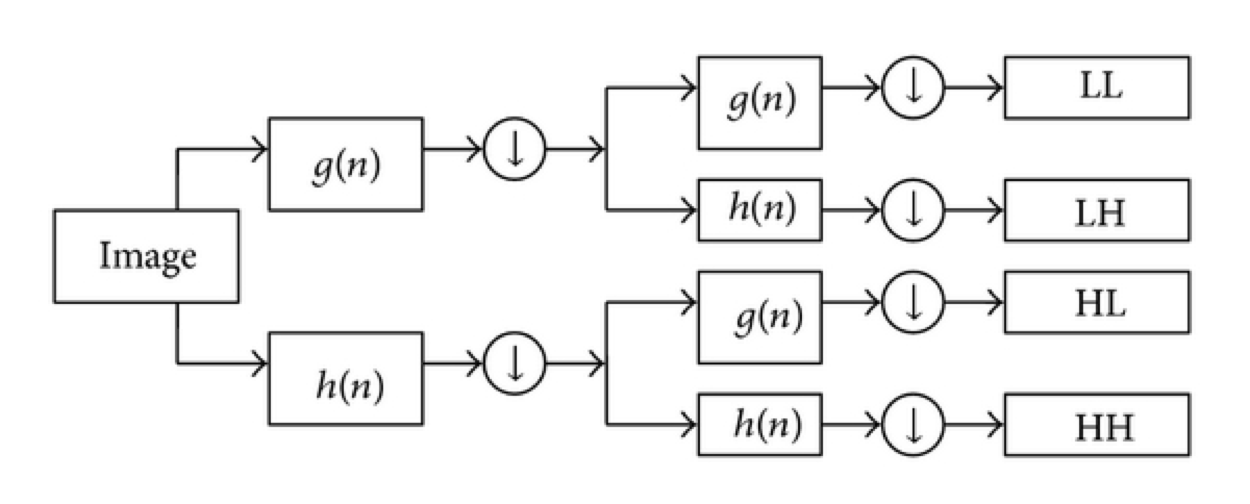
The pipeline majorly includes four image processing techniques: convolution of image with a filter as the wavelets used are essentially filters to be convoluted with the images, downsampling the image to half its size by removing alternate rows and columns from the image, element wise multiplication of image arrays and up-sampling the images to twice their sizes by using some kind of interpolation techniques.
i) Typical wavelet based edge detection based techniques involve edge detection in the HL, HH and LH transforms of an image. In their paper Edge detection by scale multiplication in wavelet domain, Zhang and Bao proposed a new method of wavelet based edge detection in which they use a product of two adjacent sub-bands (obtained by convoluting image signal with the wavelet), followed by thresholding to create a combined edge map from different scales.
If two or more edges occur in a neighborhood, they may interfere with each other. With a large scale,the dislocation of an edge will occur if there is another edge in the neighborhood. If we select a small scale parameter, the detection result would be noise sensitive.
Generally with a single scale it is very difficult to properly balance the edge dislocation and the noise sensitivity. With the scale multiplication, this problem can be largely resolved. Thus scale multiplication enhances image structures, suppresses noise and reduces the interference of neighboring edges.
ii) In this project, we have implemented the above mentioned algorithm and tested its performance in the presence of Gaussian and Impulse (salt and pepper) noises.
Two popular wavelet filters are used for the transform Haar and Coiflet. Performance of the algorithm with and without noise using the two filters is also compared.
i) We followed these steps:
-
For an image, we first calculate its subbands (LL, LH, HL, HH) using wavelet transform. If the original dimensions of the image were m*n, then each of these subband will be of the size m/2 X n/2. The HL, HH and LH bands are used for further edge detection in the later steps of the algorithm.
-
The LL subband is essentially a smaller blurred version of the original image. Wavelet transform is now performed on this image to further obtain 4 subbands of size m/4 X n/8.
-
We repeat step 2 twice to get to the m/16 X n/16 level.
-
Now that we have the edge information(LH, HL, HH) at 4 different scales, we have to combine them to get the final edges. This is done by upscaling one subband image at the lowest scale (m/16 X n/16) twice to its size and then adding it to the corresponding subband image at that scale (m/8 X n/8).
-
Step 4 is done all the way up to m X n for all the three subbands individually.
-
Now we calculate the magnitude of the LH, HL and HH to obtain our final edges.
-
Steps 1-6 are performed with different noise levels and wavelets.
ii). We have implemented the code in python and used its numpy and openCV2 libraries for image processing. We used our own implementation for wavelet transform. For noises we used an online implementation.
We acknowledge and grateful to Professor Chang Wen Chen and TAs Radhakrishna Dasari and Bhargava Urala Kota for their continuous support throughout the Course (CSE 573) that helped us learn the skills of Computer Vision and design a wavelet transform based scheme for edge detection.
Copyright {2016} {Ramanpreet Singh Khinda rkhinda@buffalo.edu and Apoorva Mittal amittal2@buffalo.edu}
Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
[1]: S. Mallat and S. Zhone. “Characterization of signals from II multiscale edges, ” IEEE Trans. PAMI, vol. 14, pp. 710732, 1992.
[2]: Y. Xu et a/, “Wavelet transform domain filters: a spatially selective noise filtration technique, ” IEEE Trans. Image Processing, vol. 3, pp. 747758,1994.
[3]: Brain M. Sadler and A. Swami, “Analysis of multiscale products for step detection and estimation, ” IEEE Trans. Information Theory. vol. 45.. D.D.. 10431051. 1999.
[4]: L. Zhang and P. Bao, “Edge detection by scale multiplication in wavelet domain,” Pattern Recognition Letters, Vol. 23, No.14, pp. 17711784, December 2002.