-
Notifications
You must be signed in to change notification settings - Fork 23
Pullup Values
Hi Chuck - confirmed - a combination of your library and properly specced pull-ups seems to be the winning combination, if I change either it freaks out and cannot recover without a hard reset (I hope this can be fixed, bit of a nightmare for unattended projects!).
Slightly related, can I ask why you suggested 1mA of drive rather than 3ma?
@chinswain The 3mA limit is the minimum drive current that must be met for the device to be 'I2C' compatible. I don't like to expect any device to run at 100% of rated performance continuously. You had stated your circuit was using 10k pullups, (0.33mA) so changing to 3.3k (1mA). this 3x increase in current caused a power consumption increase in the drive sections of your I2C devices in the amount of (I^2 ) * R. where I is current and R is resistance, so Since R is fixed for each device the power changed from (0.33^2 ) * R = 0.109 * R to (1^2) * R or 1.0 * R increasing to 3mA become 9 * R. The current increase from 0.33ma to 3.0mA is an ~10fold increase but 0.109R -> 9R is an 82 fold power increase. The benefit of the extra 2mA was not worth the load. More just makes the drivers work harder, and the increase in current does not translate into an increase in performance. The parasitic capacitance and the clock speed are the design considerations (controlling factors) for choosing the pullup values.
This webpage: RC Discharging Circuit Tutorial goes into the mathematics.
Here is a Texas Instruments Application Note SLVA689 I2C Bus Pullup Calculation on that goes into how to calculate the minimum and maximum resistance that can be used for pullup values on I2C bus. The drawback of this App Note is that it requires the Bus capacitance to be known.
I2C signals are triggered at the 30%, 70% voltage points along the curve. The formula is an exponential function Vc =Vs * e^(-t/(r * c)) Where Vc is the voltage on the buss, Vs is supply (3.3v), t is time(seconds), r is resistance(ohms), c is capacitance(Farad). You can almost solve this equation, But, that requires to you measure 'c' which is really tough on a digital circuit.
If you start selecting values: the rise time for the voltage to get to a logic High(2.3v) 70% of Vdd (3.3v). with a SCL (clock rate) of 100,000Hz to 1/10 of a clock period, t becomes 1/1,000,000 or 0.0000001S.
t=1us
Vc = 2.3v
Vs = 3.3v
e = 2.71828
r=3,300 ohm
Solve the equation for 'c'
c=-t/(r * ln(Vc/Vs))
c=8.39 * 10^-10 F or 839pF
So as long as my bus capacitance is less than ~1nf, 1mA of drive current will meet my design goals (10% rise time on a 100kHz clock).
I use 0.050" ribbon cable for my I2C interconnects. Most 28ga flat ribbon cable spec out 15pF/ft. I generally increase it an order of magnitude to 150pf/ft this takes into account the connectors, bends, surrounding objects. So with these rough guesses a 1mA drive current will handle 1m (3ft) of ribbon cable and still meet my 100kHz timing constraints. If I go to 400kHz or 800kHz. I have to adjust things.
Chuck.
I have quite a bit of reading to do to get these 40 devices working...
If you are going to attach 40 devices to the bus, you will need to actually review(measure) the signals. You can use a 'scope to calculate 'c' from the curve.
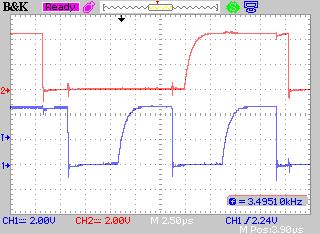
The following image show a 1.3us rise time of the SDA pulse as measured from 0V to aproximately 3.3V. The vertical cursors at 6.2us and 7.5us mark the '5tau' portion of the R/C decay curve. This 1.3us delta equates to a bus capacitance of 104pf.
 Orange is SDA, Blue is SCL.
Orange is SDA, Blue is SCL.
You can see the exponential decay on the rising edge, Those overshoots and ringing are cause by my 12" unterminated flying end of the cable. you can see the cross talk at every negative edge. Based on the 5tau infinity assumption, the 5tau is about 1.3us. currently I have 2.48k of resistance on the bus so 1.3us = 5(2480 * c), therefore c = 104pf
Chuck.