Periodic boundary conditions and simple timestepping don't combine well

[clarkpede]

Describe the bug

Periodic boundary conditions work well for steady problems and dual-time-stepping. But when I try to use time-stepping (not dual-time-stepping), the periodic boundary condition shows some artifacts. For a problem that's homogeneous in the periodic direction, the transient solution is not homogeneous in the periodic direction.

To Reproduce

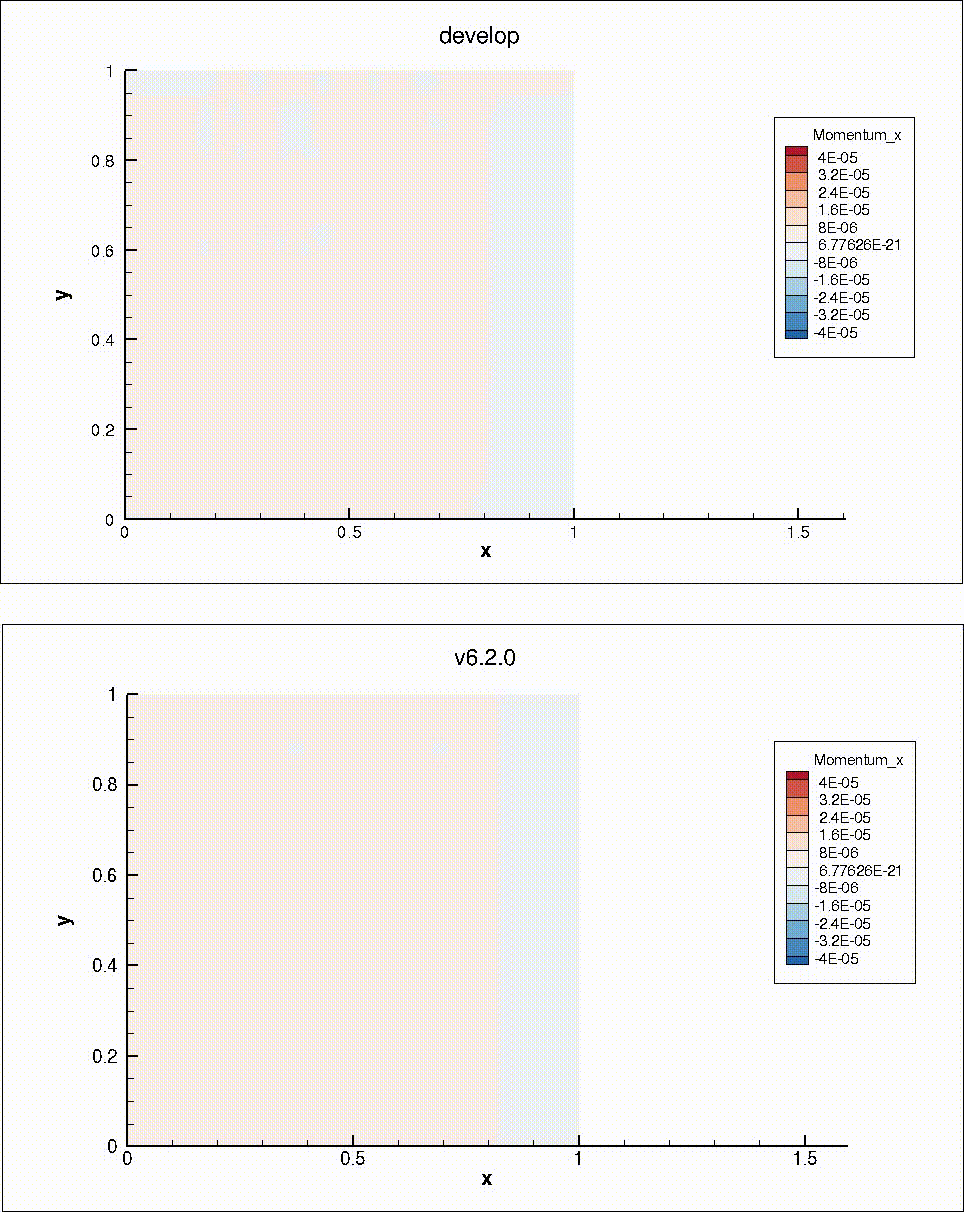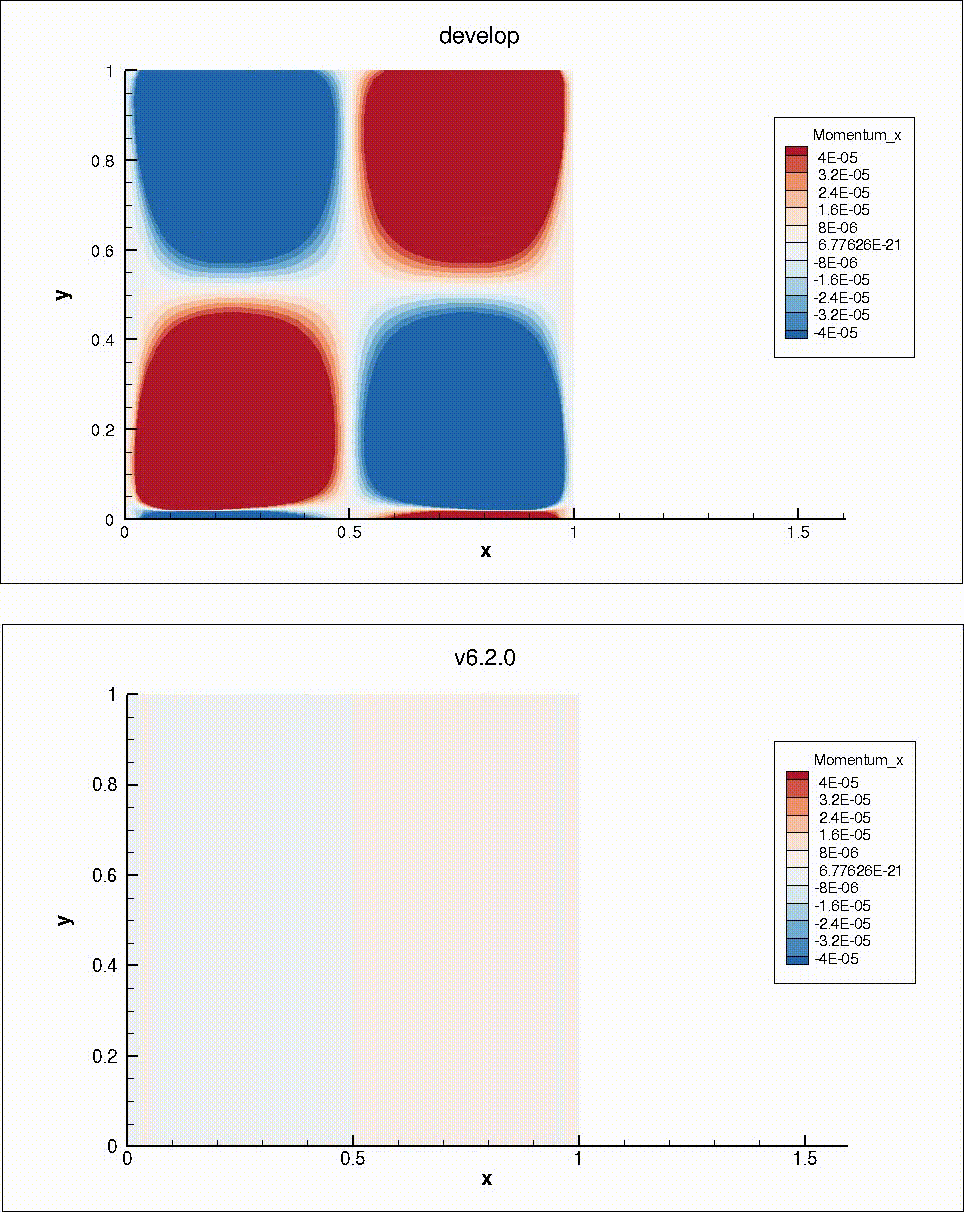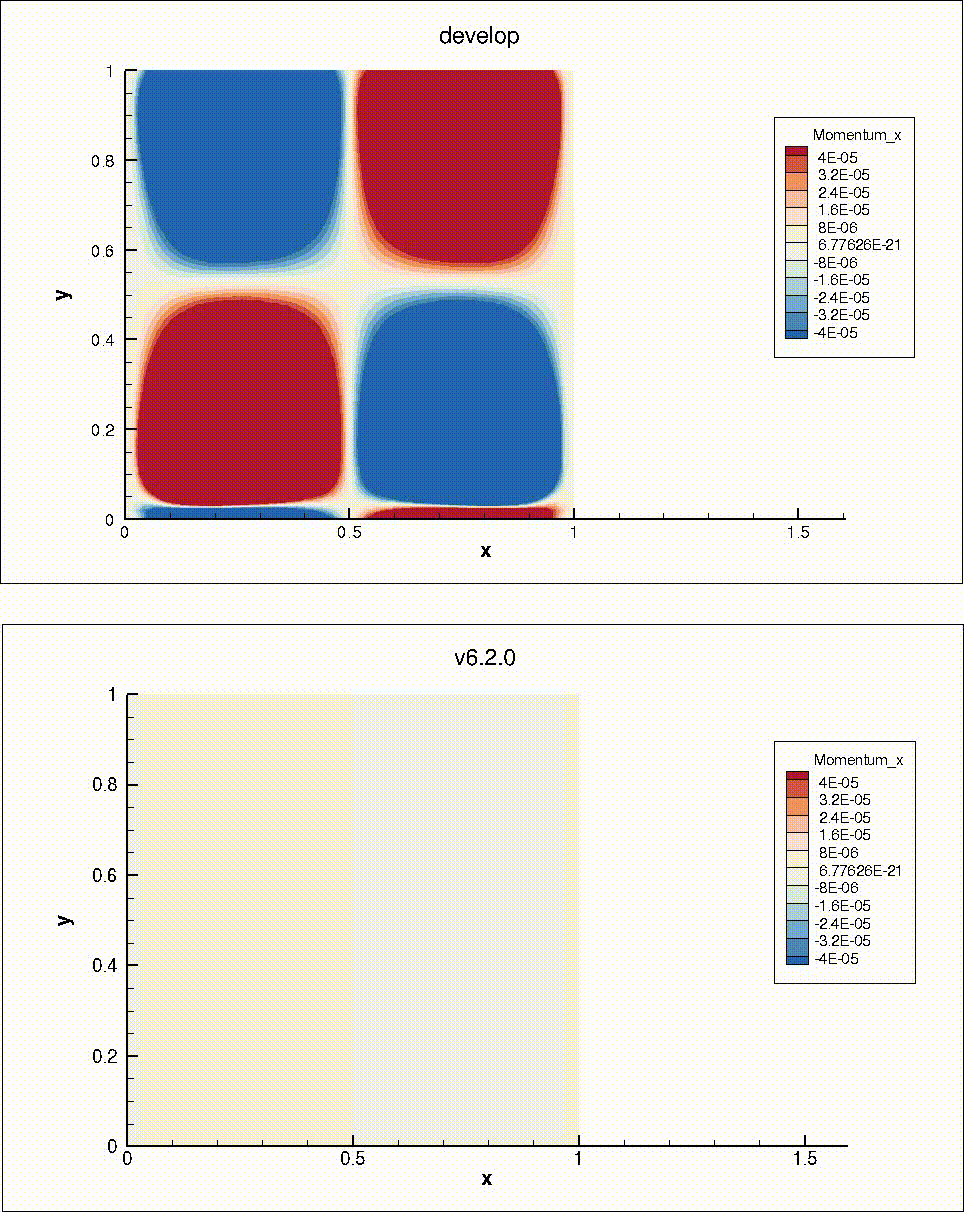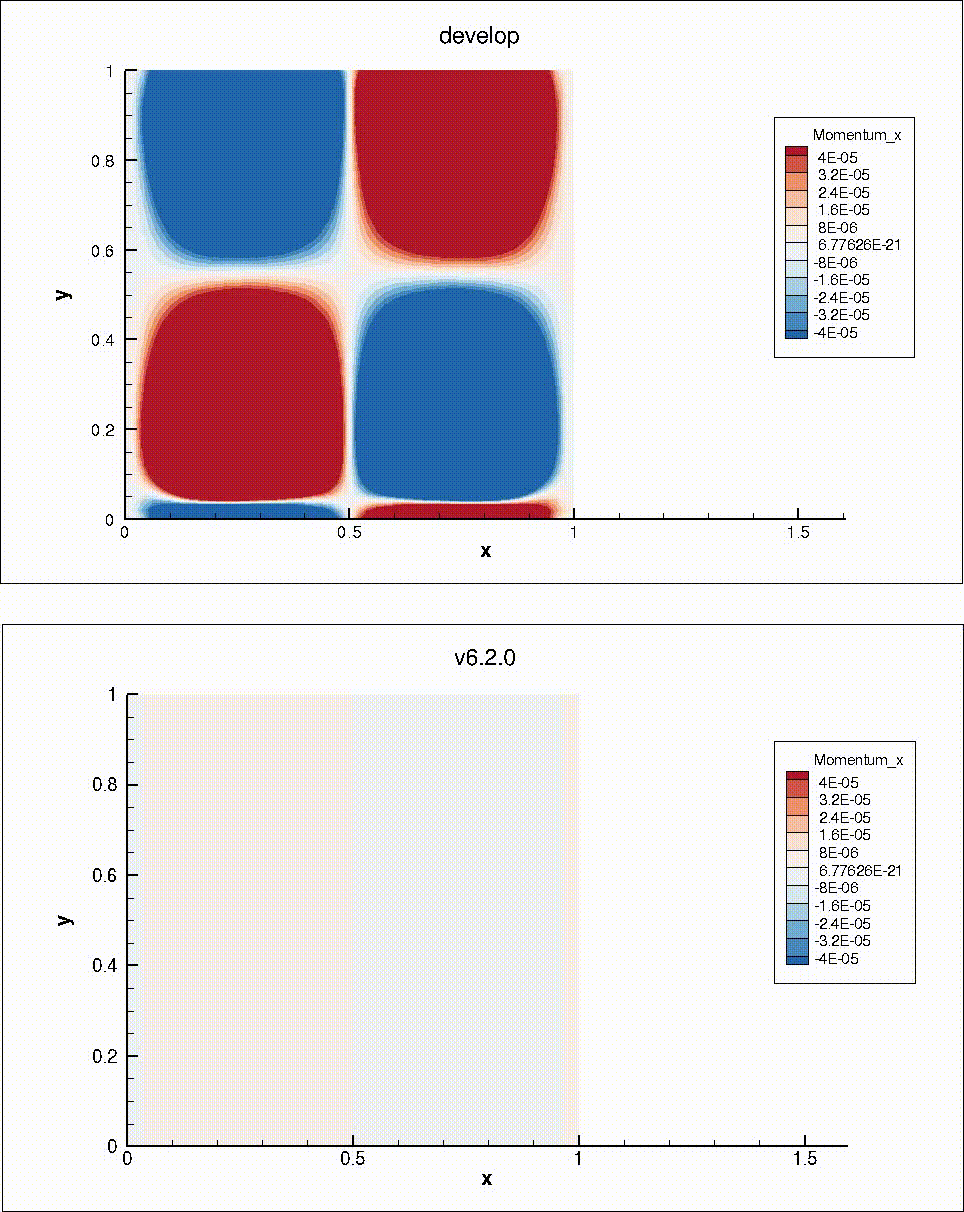
To verify the problem, I looked at the "navierstokes/poiseuille" test case. This case is homogeneous in the y direction, and has periodic boundaries. Instead of treating it as a steady-state problem, I did time-marching wit simple time-stepping. I then compared the results with the same simulation on v6.2.0 (before PR #652 changed the periodic boundaries). The y-momentum is very similar in both cases. However, the x-momentum shows inhomogeneity on the develop branch:

Here are the files to recreate my test case:
periodic_timestepping.tar.gz

My Analysis

One of my colleagues pointed out that CSolver::InitiatePeriodicComms and CSolver::CompletePeriodicComms only communicate the residual and the Jacobian of point "i" with respect to point "i". The Jacobian of point "i" with respect to point "j" is not communicated. This means that a different problem is being passed to the linear solver at the periodic nodes. In v6.2.0, a halo node approach was used, so the linear solver problem was identical for all nodes along a homogeneous direction.

If this analysis is correct, then this could be fixed by communicating the full Jacobian (with respect to all neighbors) at the periodic points.

Desktop

• OS: Ubuntu 18.04
• C++ compiler and version: icc 19.0.2.187
• MPI implementation and version: mpich2/3.2
• SU2 Version: develop branch

[economon]

Nice analysis @clarkpede. It is true that we simplify the Jacobians at the periodic boundaries, mostly to avoid issues with adding entries to the Jacobian from the neighbors that potentially do not live on our rank and to keep communication costs low (those neighbors are treated explicitly). This could be changed to communicate the full Jacobian.. but I am not sure it is worth the effort/cost.

The approximation that is made should still be consistent though, because we only allow one of the repeated periodic nodes to participate in the linear solve with each nonlinear iteration, and then we communicate its update to its periodic pair. In short, the value of the solution should always be the same on periodic points with each iteration update, and if the problem converges to a steady-state (even in time stepping mode), the Jacobian should only affect convergence (the RHS should be the same). You could try the time stepping option with one of the RK methods to see if going fully explicit helps further isolate the issue.

It could also be something related to the time step that is communicated. In the SetTime_Step() routine in the flow solver class, we do some special checks for time stepping mode to make sure that the minimum global time step is used in all cells. Might want to print out the dT communicated in the periodic comms or write the dT to the solution file to make sure everything is ok there too.

Honestly, I don't think a ton of folks use the time stepping option in general with the FVM solver, so double-checking that it behaves well for a non-periodic problem could shed some light too, unless you have already done that.

[clarkpede]

Honestly, I don't think a ton of folks use the time stepping option in general with the FVM solver.

Yeah, this problem does not fall in the normal use-case. We've found dual-timestepping very slow for turbulent problems, and had hoped to alleviate the issue by using a high-order time-stepping scheme. But we've run into several issues with time-stepping (this is one of them).

if the problem converges to a steady-state (even in time stepping mode), the Jacobian should only affect convergence (the RHS should be the same).

Unfortunately, I'm interested in scale-resolving simulations. That means I want time-accurate unsteady information. For that, consistency at a "steady state" isn't much help unless you use dual-time-stepping.

You could try the time stepping option with one of the RK methods to see if going fully explicit helps further isolate the issue.

I'll try this and see how the two branches differ.

[stale]

This issue has been automatically marked as stale because it has not had recent activity. It will be closed if no further activity occurs. Thank you for your contributions.

[clarkpede]

I have no updates here, but I also have done nothing to resolve this issue.

[stale]

This issue has been automatically marked as stale because it has not had recent activity. It will be closed if no further activity occurs. If this is still a relevant issue please comment on it to restart the discussion. Thank you for your contributions.

[clarkpede]

This is still an issue.