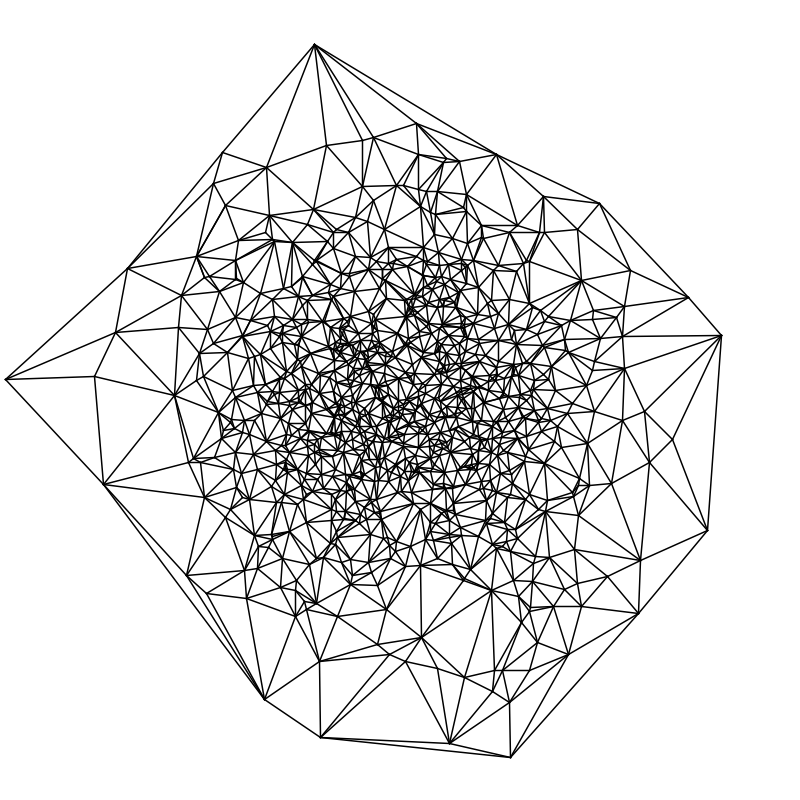
DTFE Interpolation Strategies
In order to render a continuous field using the DTFE, we interpolate between the density at the vertices using several methods.
There is typically a trade off between speed and quality.
This is an outline of the triangulation that was used to generate the DTFE interpolations.
Computed in 568 msec
This method simply locates the triangle and takes the average of the 3 densities of the triangle's vertices.
Computed in 652 msec
This method first locates the triangle, then uses the density of the closest vertex. This is essentially equivalent to the Voronoi diagram.
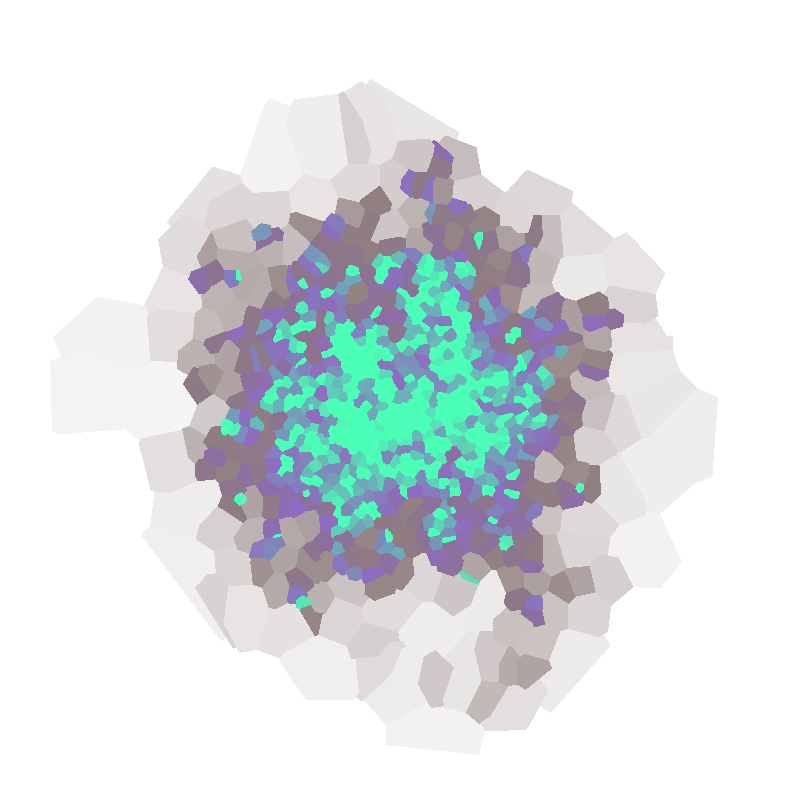
Computed in 502 msec
This method produces smooth results. It first locates the triangle, then it calculates the barycentric coordinates of the point within the triangle, and uses those coordinates as factors on the 3 densities of the triangle's vertices.
Computed in 855 msec
This method is very slow, but produces the smoothest results by far. It first creates a "2nd order voronoi cell", which is the voronoi cell which it would create if the point were added to the triangulation. Then it determines the relative overlap of that cell with the regular voronoi cells of the neighboring vertices. The final density is the sum of each neighboring vertices density weighted by its voronoi cell's overlap with the 2nd order voronoi over the area of the 2nd order voronoi.
Computed in 5,894 msec