The fort package provides convenient access to fast, structured,
random linear transforms implemented in C++ (via ‘Rcpp’) that are (at
least approximately) orthogonal or semi-orthogonal, and are often much
faster than matrix multiplication, in the same spirit as the
Fastfood, ACDC, HD and SD families
of random structured transforms.
Useful for algorithms that require or benefit from uncorrelated random projections, such as fast dimensionality reduction (e.g., Johnson-Lindenstrauss transform) or kernel approximation (e.g., random kitchen sinks) methods.
For more technical details, see the reference page for
fort().
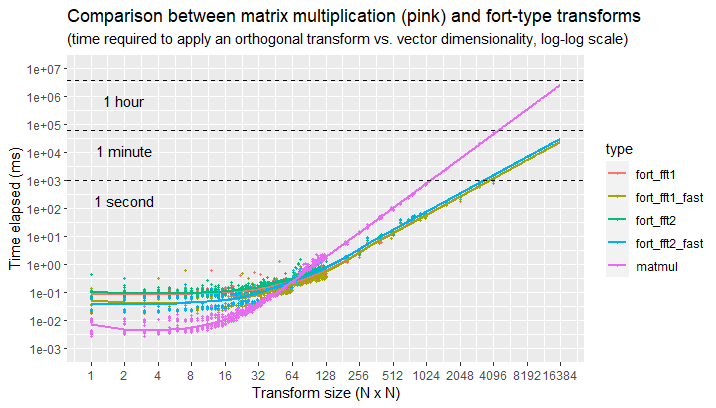
This plot shows a speed comparison between using a fort-type transform vs. a matrix multiplication, for different transform sizes, on commodity hardware.
Here we can see that, for transform sizes in spaces larger than
fort)
instead of matrix multiplication. In particular, the time elapsed can go
down by 10 to 100 times, for practical transform sizes (e.g., an
orthogonal transform in
You can install the development version of fort from
GitHub with:
# install.packages("devtools")
devtools::install_github("tomessilva/fort")Note: you will need to have the Rcpp and RcppArmadillo packages
installed, as well as a working build
environment (to compile
the C++ code), in order to install a development version of fort.
This is a basic example which shows how to use fort in practice:
library(fort)
(fast_transform <- fort(4)) # fast orthogonal transform from R^4 to R^4
#> fort linear operation: R^4 -> [fft2] -> R^4
matrix_to_transform <- diag(4) # 4 x 4 identity matrix
(new_matrix <- fast_transform %*% matrix_to_transform) # transformed matrix
#> [,1] [,2] [,3] [,4]
#> [1,] 0.7267114 -0.1421089 0.3232329 -0.5892504
#> [2,] 0.2627348 -0.7866239 -0.5065061 0.2358916
#> [3,] -0.5892504 -0.3232329 -0.1421089 -0.7267114
#> [4,] 0.2358916 0.5065061 -0.7866239 -0.2627348
(inverse_transform <- solve(fast_transform)) # get inverse transform
#> fort linear operation (inverted): R^4 <- [fft2] <- R^4
round(inverse_transform %*% new_matrix, 12) # should recover the identity matrix
#> [,1] [,2] [,3] [,4]
#> [1,] 1 0 0 0
#> [2,] 0 1 0 0
#> [3,] 0 0 1 0
#> [4,] 0 0 0 1Here is a comparison of using a fort transform against a simple matrix
multiplication, in terms of speed:
library(fort)
matrix_to_transform <- diag(1024) # 1024 x 1024 identity matrix
fast_transform <- fort(1024) # fast orthogonal transform from R^1024 to R^1024
slow_transform <- as.matrix(fast_transform) # the same, but in matrix form
# time it takes for the fast transform
system.time(for (i in 1:100) test <- fast_transform %*% matrix_to_transform, gcFirst = TRUE)
#> user system elapsed
#> 5.50 2.12 8.00
# time it takes for the equivalent slow transform (via matrix multiplication)
system.time(for (i in 1:100) test <- slow_transform %*% matrix_to_transform, gcFirst = TRUE)
#> user system elapsed
#> 70.57 0.61 77.95 Note: in this case, using a fort fast transform leads to a speed-up of
about 10x compared to the use of matrix multiplication.
For more information on how to use fort in practice, check out the
package’s
vignette.
MIT
-
Krzysztof M. Choromanski, Mark Rowland, and Adrian Weller. “The unreasonable effectiveness of structured random orthogonal embeddings.”, NIPS (2017).
-
Felix Xinnan X. Yu, Ananda Theertha Suresh, Krzysztof M. Choromanski, Daniel N. Holtmann-Rice, and Sanjiv Kumar. “Orthogonal random features.”, NIPS (2016).
-
Marcin Moczulski, Misha Denil, Jeremy Appleyard, and Nando de Freitas. “ACDC: A structured efficient linear layer.”, arXiv:1511.05946 (2015).
-
Quoc Le, Tamás Sarlós and Alex Smola. “Fastfood - approximating kernel expansions in loglinear time.”, ICML (2013).
-
Ali Rahimi, and Benjamin Recht. “Random features for large-scale kernel machines”, NIPS (2007).