Generating surfaces using a point cloud that is created from a 3d Spirograph.
A Spirograph can be described using a list of handles, each consists of a length and a rotation speed. These handles are connected to each other such that the end of handle i is the beginning of handle i + 1.
When a handle rotates, it applies its rotation to itself as well as to the rest of the handles following it.
Note that this model is much less restrictive than the original Spirograph (which was built out of gears) and therefore can create many more shapes.
left: lengths: 1.5, 0.5 ; speeds: 1.0, 2.0
right: lengths: 1.0, 1.0 ; speeds: 1.0, 1.0
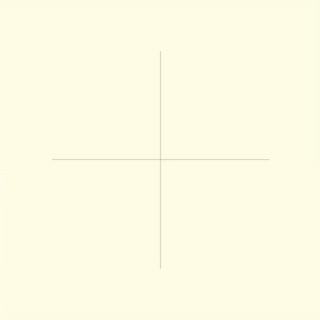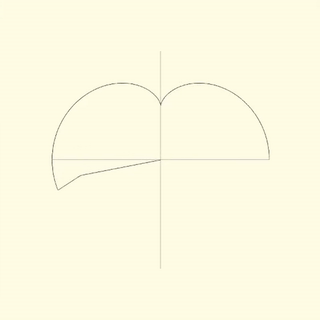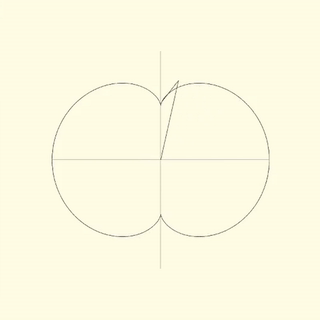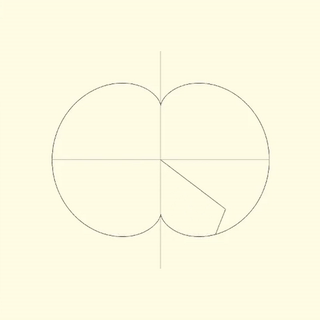

A Spirograph is defined only for 2d, so there is some ambiguity to how it should be translated to 3d. The simplest way I found was to assign a rotation axes as well as rotation speed for each handle. This model is capable of generating 2d Spirographs by setting all the rotation axes in the same direction, therefore it is clearly an extension of the original one.
In this model, the axes are encoded as <x, y, z> and the rotation speeds are their magnitudes.
left: lengths: 1.1, 0.4 ; axes: <0.0, 0.1, 0.0>, <0.0, 3.0, 0.0>
right: lengths: 0.5, 0.5, 0.5 ; axes: <1.1, 1.0, 0>, <0.0, 1.0, 1.0>, <1.0, 0.0, 1.0>


It is important to note that these 3d spirographs don't really generate surfaces, some Spirographs simply generate lines that in the limit (after many iterations) resemble surfaces.
The first step to creating a surface is generating a point cloud. The program iterates over the spirograph and places points in such a way that no two points will be too close to each other. This minimum distance is a predefined number and is important because having a too large amount of points will result in excessive computation time.
The next step is to pick three points that will create a triangle which is on the surface for sure. One way to do it would be to pick the furthest point from the center of the spirograph, and use a combination of distance and angle deviations to determine the second and third points.
Then, the algorithm recursively builds more triangles around the original one. As you can see in the code, the algorithm performs checks in order to not having two triangles share the same vertices and have almost the same normals. Although far from perfect, by handling many of these cases, the algorithm manages to generate surfaces.
left: lengths: 1.1, 0.4 ; axes: <0.0, 0.1, 0.0>, <0.0, 3.0, 0.0>
right: lengths: 0.5, 0.5, 0.5 ; axes: <1.1, 1.0, 0>, <0.0, 1.0, 1.0>, <1.0, 0.0, 1.0>

