Slipstream EMA Difficulty Algorithm

[zawy12]

Do not use this algorithm

The problem is that there is a sweet spot in attacking, shown here:

==================
Come back to check before doing any pull or merge. Code compiles and is currently on 2 to 5 testnets. Hopefully the testnets will concur with my spreadsheet today 5/22/2018.

Change history:
5/21/2018:

• 11:00 am was first version
• 7:10 pm fixed ROP()
• 9:00 pm removed errant dots in timestamps.[N] and difficulties.[N]
• 9:35 pm ROP() fix reverted and specifying D must be >100 , L(0) removed

5/22/2018:

• 6:35 am Name change from Fuzzy EMA to EMA2. ROP() finally correct.
• 8:55 am Copy-pasted Technohacker's monero code of this which had minimal modifications to compile.
• 11:15 am Technohacker testnet is oscillating. Removing 1-block delay in D calculation.
• 5:00 pm Changed the 3 core formulas to need only 1 division as part of ROP
• 6:30 a division 1/1.14 was converted to multiplication 0.877 as part of ROP.

There were some instances where LWMA was not performing optimally see LWMA failures. This is an attempt to solve the problem. Large coins should use the Simple EMA. This one should be the best for small coins. This supersedes LWMA, D-LWMA, and Dynamic EMA.

// Cryptonote coins must make the following changes:
// const uint64_t CRYPTONOTE_BLOCK_FUTURE_TIME_LIMIT   = 3xT;  // (360 for T=120 seconds)
// const size_t   BLOCKCHAIN_TIMESTAMP_CHECK_WINDOW  = 11;
// const unit64_t DIFFICULTY_BLOCKS_COUNT  = DIFFICULTY_WINDOW + 1
// Make sure lag is zero and do not sort timestamps.
// CN coins must also deploy the Jagerman MTP Patch. See:
// https://github.com/loki-project/loki/pull/26#event-1600444609

Slipstream EMA Description
Slipstream EMA estimates current hashrate in order to set difficulty to get the correct solvetime. It gives more weight to the most recent solvetimes. It is designed for small coin protection against timestamp manipulation, hash-attacks, delays, and oscillations. It rises 10% per block when an attack begins, so most attacks can't benefit from staying on more than 2 blocks. It uses a very fast Exponential Moving Average to respond to hashrate changes as long as the result is within a +/- 14% range around a slow tempered Simple Moving Average. If it goes outside that range, it switches to a medium-speed EMA to prevent it from rising too high or falling too far. Slipstream refers to it having a strong preference to being "behind" the SMA within +/- 14%. It resists going outside that range, and is anxious to return to it.

// Slipstream EMA difficulty algorithm
// Copyright (c) 2018 Zawy
// EMA math by Jacob Eliosoff and Tom Harding.
// https://github.com/zawy12/difficulty-algorithms/issues/27
// Cryptonote-like coins must see the link above for additional changes.

// Round Off Protection. D must normally be > 100 and always < 10 T.
// This is used because some devs believe double may pose a round-off risk.
double ROP(double RR) {
      if( ceil(RR + 0.01) > ceil(RR) )   {   RR = ceil(RR + 0.03);   }
      return RR;
 }
difficulty_type next_difficulty(std::vector<std::uint64_t> timestamps, 
     std::vector<difficulty_type> cumulative_difficulties, size_t target_seconds)    {
     // After startup, timestamps & cumulative_difficulties vectors should be size N+1.
     double T = target_seconds;
     double N = DIFFICULTY_WINDOW; //  N=60 in all coins.
     double FTL = CRYPTONOTE_BLOCK_FUTURE_TIME_LIMIT; // < 3xT
     double next_D, ST, D, tSMA, sumD, sumST;

     // For new coins height < N+1, give away first 4 blocks or use smaller N
     if (timestamps.size() < 4) { return 100; }
     else if (timestamps.size() < N+1) { N = timestamps.size() - 1; }
     // After startup, the following should be the norm.
     else { timestamps.resize(N+1); cumulative_difficulties.resize(N+1); }

     // Calculate fast EMA using most recent 2 blocks.
     // +6xT prevents D dropping too far after attack to prevent on-off attack oscillations.
     // -FTL prevents maliciously raising D.  ST=solvetime.
     ST = std::max(-FTL, std::min(double(timestamps[N] - timestamps[N-1]), 6*T));
     D = cumulative_difficulties[N] - cumulative_difficulties[N-1];
     next_D = ROP( D*9*T / (8*T+ST*1.058) );

     // Calculate a 50% tempered SMA. 
     sumD = cumulative_difficulties[N] - cumulative_difficulties[0];
     sumST = timestamps[N] - timestamps[0];
     tSMA = ROP( sumD*2*T / (N*T+sumST) );

     // Do slow EMA if fast EMA is outside +/- 14% from tSMA. 0.877 = 1/1.14.
     if (next_D > tSMA*1.14 || next_D < tSMA*0.877) {
         next_D = ROP( D*28*T / (27*T+ST*1.02) );
     }
     return static_cast<uint64_t>(0.9935*next_D);
}

Stable hash rate comparison

Typical attack comparison

Attacks that cause oscillations

Notice how much higher Digishield goes, causing delays.

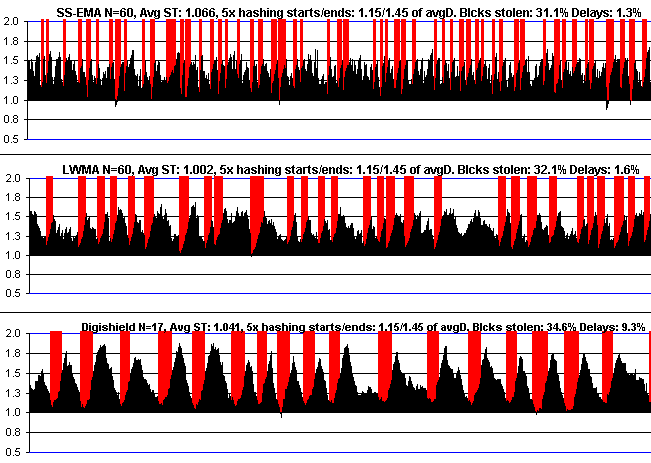
Justification for each setting

I'm against a dev such as myself selecting any constant in difficulty algorithms. It should be an objective setting. But due to the non-linearity of of miners jumping on or off based on some rough threshold (like +/- 25%), and based on miners being able to change behavior when the algorithm can't, it's mathematically difficult to develop an algorithm that can figure out the best settings. It seems to need a an A.I. Lacking the skill, I've needed to rely on experience and observation to choose several settings. These are supposedly close to what an A.I. would conclude Some of the constants are not chosen by me other than to do the correct math, but the important ones are. The important ones are 6xT ,+/- 14%, N=60, 50%, N=28, and N=9.

• ROP is based on"double" being at least 15 digits in precision. It seemed conceivable coins using this algo could have Difficulty as high as 9.999 T which would place the 15th digit at 0.01. Smaller D can still have round-off error.
• Certain small adjustments were needed to get more accurate avg ST because the EMA equation here is simplified to prevent e^x calculations. They are: 0.98, 0.945, and 0.9935.
• FTL limit allows max 15% drop in D for only 1 block in EMA N=9 that can't be repeated for 20 blocks or work when EMA N=28 is active. Smaller value may pose risk to network.
• 6xT limits how far D can drop when a hash attack ends. It's a balance between wanting D to drop quickly, but not too far that it would invite hash attack oscillations. It is large enough to not affect calculations under normal mining conditions.
• N=60 used in the 50% tempered SMA will vary approximately +/- SQRT(1/(60/.50) = 9% every 120 blocks. It's a balance between wanting to capture recent changes in hash rate ( 60 =~ 3 hours for T=120 coins) but not accidentally varying so much that it will encourage on-off mining. 50% tempering acts a little like Digishield's 75% tempering that does better than a simple SMA by responding more quickly to recent changes with less accidental variation. I chose half-way between SMA and Digishield based an intuitive viewpoint. The 9% is not too arbitrary. It's based on my opinion of how quickly price+fees and hash rate change every few hours, and how much on-off miners will be motivated to start or stop when it accidentally goes -9% or +9%. It is 3x slower than EMA N=28 which is 3x slower than EMA N=9.
• +/- 14% fast variation limit is based on wanting to be large enough to counter any +/- 9% motivations but not vary so much it overshoots difficulty that could result in excessive delays. It's based the "observational belief" that the total 28% fast response range is enough to stop most miners who are trying to pick a low D to start mining....in only 3 blocks thanks to the fast response. Dedicated miners will probably accept constant +/- 14% changes as no problem. It's easier to jump back into the 14% range via the fast EMA, than it is go far outside of it.
• There is an N=9 in the fast EMA that is also where the "8" comes from. It's value is based on wanting to change 10% per block, not more or less. This is based on seeing miners jumping on "N=60" algorithms when D is < 15% low and jumping off after it has risen 20% to 30%, typically taking 15 to 25 blocks for the DA to respond. This dis-motivates them in 3 blocks. It is also chosen as something that is 3x faster than the "governing" medium-speed EMA (see next item).
• The medium speed EMA with N=28 is chosen to act with the same speed as LWMA which is about 25% faster than Digishield's 75% tempered SMA N=17. LWMA N=60 was chosen based on observing Digishield needed to be a little faster and that SMA's with N=35 were about as low as SMA's could go due to instability from low N (which attracts on-off mining). The stability of LWMA N=60 and EMA N=28 is about like an SMA N=40, so it's clearly faster than digishield while not varying enough to attract on-off mining.

[zawy12]

Code from other coins for my future reference:
Niobio

difficulty_type Currency::nextDifficultyV5(std::vector<uint64_t> timestamps, std::vector<difficulty_type> cumulativeDifficulties) const {
		// Slipstream EMA difficulty algorithm
		// Copyright (c) 2018 Zawy
		// EMA & LWMA math by Jacob Eliosoff and Tom Harding.
		// https://github.com/zawy12/difficulty-algorithms/issues/27
		// Cryptonote-like coins must see the link above for additional changes.
		// After startup, timestamps & cumulativeDifficulties vectors should be size N+1.
		double N = CryptoNote::parameters::DIFFICULTY_WINDOW_V4 - 1;
		double T  = m_difficultyTarget;
		double FTL = static_cast<int64_t>(CryptoNote::parameters::CRYPTONOTE_BLOCK_FUTURE_TIME_LIMIT_V5);
		double next_D, ST, D, tSMA, sumD, sumST;

		if (timestamps.size() >= (N + 1)) {
			// After startup, the following should be the norm.
			timestamps.resize(N + 1); cumulativeDifficulties.resize(N + 1);
			// For new coins height < N+1, give away first 4 blocks or use smaller N
		} else if (timestamps.size() >= 4) {
			N = timestamps.size() - 1;
		} else {
			return 100;
		}

		// Calculate fast EMA using most recent 2 blocks.
		// +6xT prevents D dropping too far after attack to prevent on-off attack oscillations.
		// -FTL prevents maliciously raising D.  ST=solvetime.
		ST = std::max(-FTL, std::min(double(timestamps[N] - timestamps[N - 1]), 6 * T));
		D  = cumulativeDifficulties[N] - cumulativeDifficulties[N - 1];
		next_D = roundOffProtection(D * 9 * T / (8 * T + ST * 1.058));

		// Calculate a tempered SMA.
		sumD = cumulativeDifficulties[N] - cumulativeDifficulties[0];
		sumST = timestamps[N] - timestamps[0];
		tSMA = roundOffProtection(sumD * 2 * T / (N * T + sumST));

		// Do slow EMA if fast EMA is outside +/- 14% from tSMA.
		if (next_D > (tSMA * 1.14) || next_D < (tSMA * 0.877)) {
			next_D = roundOffProtection(D * 28 * T / (27 * T + ST * 1.02));
		}
		return static_cast<uint64_t>(0.9935 * next_D);
	}

Wownero

// Slipstream EMA difficulty algorithm
// Copyright (c) 2018 Zawy
// EMA math by Jacob Eliosoff and Tom Harding.
// https://github.com/zawy12/difficulty-algorithms/issues/27
// Cryptonote-like coins must see the link above for additional changes.

// Round Off Protection. D must normally be > 100 and always < 10 T.
// This is used because some devs believe double may pose a round-off risk.
double ROP(double RR) {
      if( ceil(RR + 0.01) > ceil(RR) )   {   RR = ceil(RR + 0.03);   }
      return RR;
 }
difficulty_type next_difficulty_v3(std::vector<std::uint64_t> timestamps, std::vector<difficulty_type> cumulative_difficulties) {
     // After startup, timestamps & cumulative_difficulties vectors should be size N+1.
     double N = DIFFICULTY_WINDOW_V2;
     double T = DIFFICULTY_TARGET_V2;
     double FTL = static_cast<int64_t>(CRYPTONOTE_BLOCK_FUTURE_TIME_LIMIT_V3); // < 3xT
     double next_D, ST, D, tSMA, sumD, sumST;

     // For new coins height < N+1, give away first 4 blocks or use smaller N
     if (timestamps.size() < 4) { return 100; }
     else if (timestamps.size() < N+1) { N = timestamps.size() - 1; }
     // After startup, the following should be the norm.
     else { timestamps.resize(N+1); cumulative_difficulties.resize(N+1); }

     // Calculate fast EMA using most recent 2 blocks.
     // +6xT prevents D dropping too far after attack to prevent on-off attack oscillations.
     // -FTL prevents maliciously raising D.  ST=solvetime.
     ST = std::max(-FTL, std::min(double(timestamps[N] - timestamps[N-1]), 6*T));
     //  Most recent solvetime applies to previous difficulty, not the most recent one.
     D = cumulative_difficulties[N] - cumulative_difficulties[N-1];
     next_D = ROP(D*9/(8+ST/T/0.945));

     // Calculate a tempered SMA. Don't shift the difficulties back 1 as in EMA.
     sumD = cumulative_difficulties[N] - cumulative_difficulties[0];
     sumST = timestamps[N] - timestamps[0];
     tSMA = ROP(sumD/(0.5*N+0.5*sumST/T));

     // Do slow EMA if fast EMA is outside +/- 14% from tSMA.
     if (next_D > tSMA*1.14 or next_D < tSMA/1.14) {
         next_D = ROP( D*28/(27+ST/T/0.98));
     }
     return static_cast<uint64_t>(0.9935*next_D);
   }
}

Technohacker

difficulty_type next_difficulty(std::vector<std::uint64_t> timestamps, std::vector<difficulty_type> cumulative_difficulties, size_t target_seconds) {
     // After startup, timestamps & cumulative_difficulties vectors should be size N+1.
     double N = DIFFICULTY_WINDOW;
     double T = target_seconds;
     double FTL = static_cast<int64_t>(CRYPTONOTE_BLOCK_FUTURE_TIME_LIMIT);
     double next_D, ST, D, tSMA, sumD, sumST;

     // For new coins height < N+1, give away first 4 blocks or use smaller N
     if (timestamps.size() < 4) { return 100; }
     else if (timestamps.size() < N+1) { N = timestamps.size() - 1; }
     // After startup, the following should be the norm.
     else { timestamps.resize(N+1); cumulative_difficulties.resize(N+1); }

     // Calculate fast EMA using most recent 2 blocks.
     // +6xT prevents D dropping too far after attack to prevent on-off attack oscillations.
     // -FTL prevents maliciously raising D.  ST=solvetime.
     ST = std::max(-FTL, std::min(double(timestamps[N] - timestamps[N-1]), 6*T));
     //  Most recent solvetime applies to previous difficulty, not the most recent one.
     D = cumulative_difficulties[N-1] - cumulative_difficulties[N-2];
     next_D = ROP(D*9/(8+ST/T/0.945));

     // Calculate a tempered SMA. Don't shift the difficulties back 1 as in EMA.
     sumD = cumulative_difficulties[N] - cumulative_difficulties[0];
     sumST = timestamps[N] - timestamps[0];
     tSMA = ROP(sumD/(0.5*N+0.5*sumST/T));

     // Do slow EMA if fast EMA is outside +/- 14% from tSMA.
     if (next_D > tSMA*1.14 or next_D < tSMA/1.14) {
         next_D = ROP( D*28/(27+ST/T/0.98));
     }
     return static_cast<uint64_t>(0.9935*next_D);
  }