-
Notifications
You must be signed in to change notification settings - Fork 30
Open
Description
Hi, it is really a nice paper. But I have a question.
May I know why you need to use Eq. (7) and (8) to approximate the posterior?
My idea is that in the E-step, you need to identify k rules with the best quality.
Since 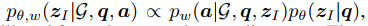
you can simply calculate prior x likelihood for each rule in z_hat, and choose the top-k rules.
But what you do is to calculate the H(rule) for each rule and choose the top-k rules.
Since H(rule) is a approximate of the posterior distribution which is proportion to prior x likelihood, it will have the same effect as using prior x likelihood.
It seems to me that all the proof and proposition in Section 3.3 E-step is unnecessary.
Metadata
Metadata
Assignees
Labels
No labels