Robinson Foulds Distance

Computing the Robinson-Foulds Distance

The very straight forward way to compute the Robinson-Foulds (RF) distance, or symmetric difference, is using the following instruction:

PLL_EXPORT unsigned int pll_utree_rf_distance(pll_utree_t * t1,
                                              pll_utree_t * t2,
                                              unsigned int n_tips);

pll_utree_rf_distance takes 2 trees as input plus the number of tips, and returns directly the RF distance. See the section below for details about important constraints for both trees.

However, if we want to compare one single tree several times (e.g., computing all pairwise distances on a large set of trees), pll_utree_rf_distance will add an important computational overhead since the split sets are created and destroyed every time it is called. A lower level approach is computing the split sets for the trees and compare them:

-1. Create the splits for the trees:

PLL_EXPORT pll_split_t * pll_utree_split_create(pll_utree_t * tree,
                                                unsigned int n_tips,
                                                unsigned int * n_splits);

-2. Get the RF distance from the splits:

PLL_EXPORT unsigned int pll_utree_split_rf_distance(pll_split_t * s1,
                                                    pll_split_t * s2,
                                                    unsigned int n_tips);

-3. Destroy the splits:

PLL_EXPORT void pll_utree_split_destroy(pll_split_t * split_list);

1. Splitting the tree

The first step is computing the bipartitions (or splits) of each tree. Let's assume we start with the following tree:

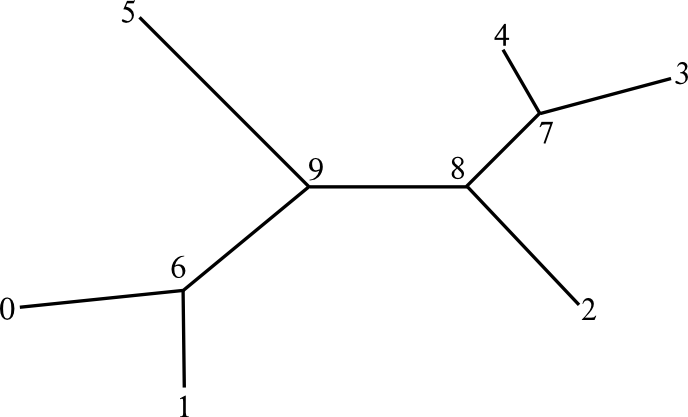
Numbers in nodes are the node id's, and there are 2 constraints here in how the node ids must be set:

1. Node ids must be sequential from 0 to (2n-3), where n is the number of tip nodes.
2. Ids from 0 to (n-1) are reserved for tip nodes.
3. Node ids at the tip nodes must agree between both compared trees (i.e., tip i is matched with the same taxon in both trees).

We can validate these conditions using the following function:

PLL_EXPORT int pll_utree_consistency_check(pll_utree_t * t1,
                                           pll_utree_t * t2,
                                           unsigned int n_tips);

Or, we can enforce them if there is no inconvenience in changing the node ids:

PLL_EXPORT int pll_utree_consistency_set(pll_utree_t * t1,
                                         pll_utree_t * t2,
                                         unsigned int n_tips);

Every branch can split the tip nodes in 2 subsets. Splits on tip branches are called trivial bipartitions. Internally, each branch is a bitvector with length equal to the number of tips, having bit at position i reserved for tip with id i. Bits in the split have values '0' or '1', depending on which side of the branch we can find the correspondent tip. There is no direction in this assignment, so the split s is identical to ~s (e.g., 010110 == 101001). First, we define the trivial bipartitions (which won't be part of our final split set, since they are identical in all possible trees sharing the same taxa).

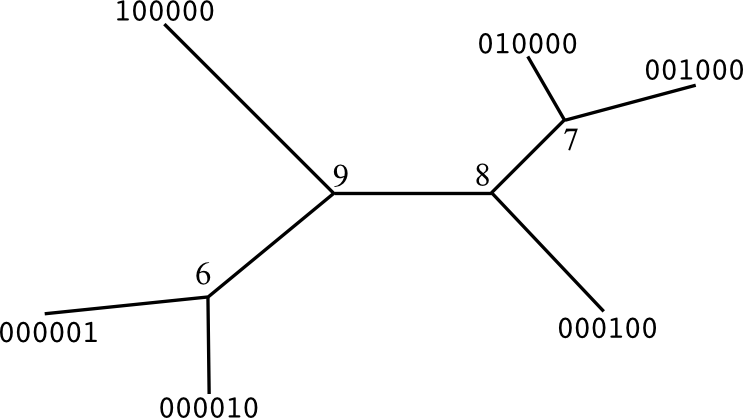
Next, starting at any arbitrary inner node, we compute a postorder traversal focusing on the inner branches. Inner branches will define our final split set.

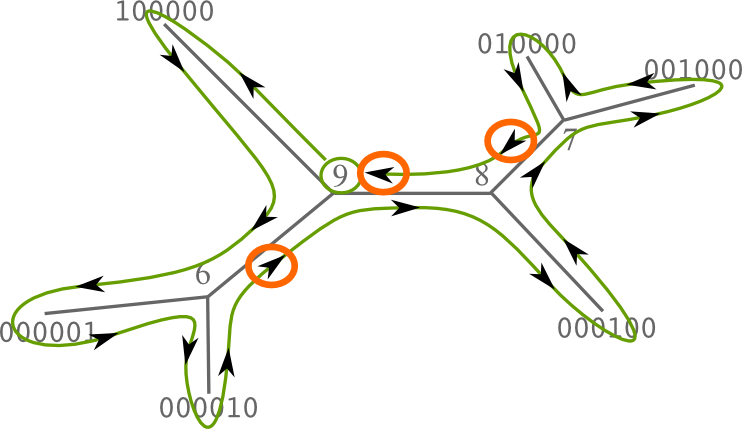
For each inner branch, we define as children the 2 connected branches that were already traversed. The split at the current branch is the sum, or the logical OR, of the 2 children splits. Next picture shows how the splits are calculated according to the previous traversal descriptor.

Finally, we have the set of splits for the current tree. According to the picture above, 000011, 011000 and 011100.

Split normalization

In order to compare them easily, we say that the splits are normalized when a certain position has always the same value. For example, we can force position of tip 0 (last position) to be always 0 in the bitvectors. Therefore, the 3 splits would be normalized as 111100, 011000 and 011100.

2. Comparing the split sets

Once the split sets for both trees were created and normalized, the Robinson-Foulds distance is the count of the non-shared splits. For example:

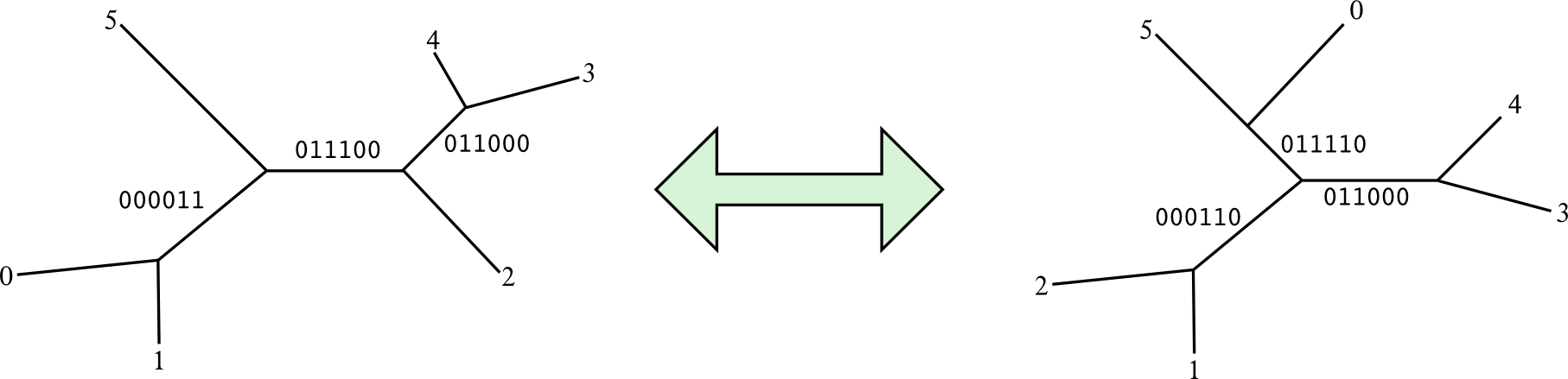
We have he following normalized split sets: S(t1) = {111100, 011000, 011100} and S(t2) = {000110, 011110, 011000}. Split 011000 is shared between both trees. The remaining splits are S(t1 x t2) = {111100, 011100, 000110, 011110}. Therefore, the Robinson-Foulds distance between t1 and t2 is 4.