AdderSR

AdderSR：Towards Energy Efficient Image Super-Resolution 【华为 cvpr2021】

paper地址

机器之心 论文详解-视频

未复现，而且论文没有展示代码运行速度结果比较，结果只是说 计算能量消耗降低了,远远小于乘法

研究问题

第一个超分辨率的卷积神经网络(SRCNN)只包含三个具有大约57K参数的卷积层。然后，随着深度和宽度的增加，DCNN的容量被放大，导致超分辨率的显著提高。但DCNN的参数和计算成本也相应增加。

例如，剩余密集网络(RDN)包含22M参数，并且仅处理一个图像需要大约10192GFLOP（浮数操作 每秒10亿次的浮点运算数 CPU性能参数 越高越好）。

本文利用加法神经网络(AdderNet)研究了单幅图像超分辨率问题。与卷积神经网络相比，加法网利用加法计算输出特征，避免了传统乘法的大量能量消耗。

文章流程

1、AdderNet应用在超分出现的问题：

​ ①加法器操作不容易学习一致性映射，输入和输出特征之间的相似性；

​ ②AdderNet无法保证高通滤波器【除去图像的低频部分】的功能。

2、分析两个问题出现的原因并进行证明

3、提出解决方案

4、实验验证

核心方案

• 利用类似残差的方法解决无法实现一致性映射的问题

  解决方案简单粗暴 $y=x+f(x)$

  加法神经网络：采用曼哈顿距离度量，结果为 对位核减去输入的绝对值 的负数 的加值

  

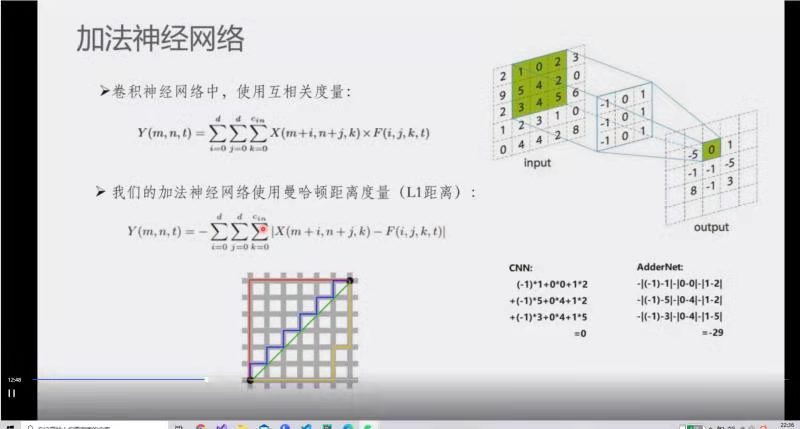
  需要注意 负号、绝对值 位置

  • 单层加法网络无法学习恒等映射。不存在W满足$I_y=I_y⊕W$ 此处的$I_y$ 和W表示矩阵.

    公式推导:

    

  解决方案：每层加法操作加入shortcut ,辅助加法操作: $Y^l=X^l+W^l⊕X^l$

  结果如下,比较值为PSNR,

  

• 利用指数激活解决无法实现高通滤波(无法消除低频信息,获取高频纹理) 的问题

  单层加法网络无法学习高通滤波 $Φ(I)=Φ(I_H+I_L)=σ(I_H)$,以提取图像中的高频信息.具体的对于低频信息E(全1单位矩阵),不存在权重W使得:$(s*E)⊕W=a $,其中s为任意常数,a为固定某个数

  推导公式见图:

  

  解决方案如下:

  提出可以学习的幂激活函数,位于加法层和BN层之后:$\mathcal{P}(\mathbf{Y})=\operatorname{sgn}(\mathbf{Y}) \cdot|\mathbf{Y}|^{\alpha}$

  • 当α > 1 时,函数可以增强输出图像的对比度,并强调高频信息.

  • 当0< α < 1时,函数可以平滑输出图像中的所有信号,并消除伪影和噪声.

  **需要注意 α初始化 需大于 0 ** 当α小于0 时结果会非常差

  学到图像边缘信息的结果对比如下,比较值为PSNR:

  

  增加一个power activation，即$f(x)=sign(x)·|x|^γ$

消融实验说明 恒等变换非常重要，幂激活函数 有了更好。

结果明显表示 加法 和 乘法 的结果准确率结果差不多,加法的乘法计算明显下降.

表3 为 在不同剪枝率操作的结果比较 ,能耗降低 准确率下降较低

​ ×2 规模 下不同网络的能耗。使用720p高分辨率图像计算能源成本。消耗是有所下降。

疑惑 此处有个疑问,乘法计算降低了可加法计算增多了,有区别吗.

**** 找了一些资料

CPU内部实现加减乘除的过程 博客

与芯片面积有关,只部署加法和少量乘法系,芯片面积就会远小于乘法网络.

加法在不同比特的能耗明显小于乘法,与芯片面积有关,作者贴了图

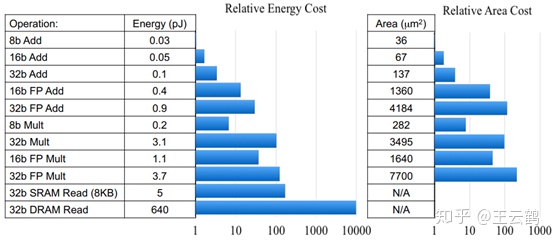
实验结果:

作者工作

​ 深入分析了加法器操作与身份映射之间的关系，并插入快捷方式，以提高使用加法器网络的SR模型的性能。

​ 开发一个可学习的power activation，以调整特征分布和细化细节。

​ 使用加法网络的图像超分辨率模型可以实现与其CNN基线相当的性能和视觉质量，并使能耗降低约2×。

附带论文

AdderNeet:Do We Really Need Multiplications in Deep Learning?

论文地址：paper

代码实践：code

​ AdderNet 利用加法计算输出特征，避免了传统乘法的大量能量消耗

​ 利用加法运算代替乘法来减少网络的消耗。在卷积层中没有使用乘法，在分类任务上实现了边际精度损失。

​ 使用$L_1$距离来度量神经网络中特征和滤波器之间的相关性。

​ 设计带有自适应学习率的改进梯度计算方案，确保滤波器的优化速度和更好的网络收敛。

结果：

​ 在CIFAR和ImageNet数据集上的结果表明AdderNet可以在分类任务上取得和CNN相似的准确率。

### 加法

​ 给定神经网络的卷积核$F∈R^{d×d×C_{in}×C_{out}}$,其中d为卷积核的大小,$C_{in}$和$C_{out}$分别为输入和输出通道数,输入特征为$X∈R^{H×W×C_{in}}$,其中H 和 W 为特征的长和宽,输出特征可以被计算为:

$Y(m, n, t)=\sum_{i=0}^{d} \sum_{j=0}^{d} \sum_{k=0}^{c_{i n}} S(X(m+i, n+j, k), F(i, j, k, t))$

其中S(·,·)是距离度量函数,当使用互相关作为距离度量时，我们有$S(x,y)=x×y$ ，此时上面的公式就成为了卷积运算，当$d=1$时，公式可以被看做全连接层的计算。事实上，除了互相关以外，还有很多其他的度量函数可以提取滤波器和输入特征之间的关系，但是，大部分的度量函数都包含乘法，因此带来了大量的计算代价。

因此，我们希望使用一种只具有加法的度量函数，即L1距离，来代替卷积神经网络中的卷积计算。通过使用L1距离，输出的特征可以被重新计算为：

$Y(m, n, t)=\sum_{i=0}^{d} \sum_{j=0}^{d} \sum_{k=0}^{c_{i n}} |X(m+i, n+j, k)-F(i, j, k, t)|$

可以看到，公式中的计算只需要使用加法，通过将卷积中计算特征的度量方式改为L1距离，我们可以只使用加法来提取神经网络中的特征，并构建加法神经网络.

优化方案

神经网络使用反向传播来计算参数的梯度，再通过梯度下降来对网络中的参数进行优化。在Addernet中，输出特征Y对滤波器F的偏导数为：

$\frac{\partial Y(m, n, t)}{\partial F(i, j, k, t)}=\operatorname{sgn}(X(m+i, n+j, k)-F(i, j, k, t))$

其中sgn 代表符号函数。

可以看到，偏导数的输出结果为+1,0或-1，仅有三个值的输出，不能很好的反应输入特征X和滤波器F之间的距离关系，也不利于滤波器的优化。于是，我们考虑将求导公式中的符号函数去掉：

$\frac{\partial Y(m, n, t)}{\partial F(i, j, k, t)}=X(m+i, n+j, k)-F(i, j, k, t)$

使用改进方式计算的梯度更能表达输入特征和滤波器之间的距离大小关系，也更加有利于梯度的优化，于是我们使用该公式的计算结果来优化滤波器。

特别地，由于使用改进梯度计算出的结果的量级可能大于1，在对输入特征X求偏导数时，我们对其进行截断：

$\frac{\partial Y(m, n, t)}{\partial X(m+i,n+ j, k)}=HT(F(i,j,k,t)-X(m+i, n+j, k))$

其中HT为HardTanh函数，即将输出截断到-1到+1。如果不对X进行截断，多层的反向传播会使得改进梯度的量级和真实梯度的量级有着很大的累计误差，导致梯度爆炸。

自适应学习率调整

在传统CNN中，我们常常希望每一层之间的输出分布相似，使得网络的计算更加稳定考虑输出特征的方差，我们假设X和F都为均值0的标准正态分布，在CNN中的方差可以被计算为：

$\begin{aligned} \operatorname{Var}\left[Y_{C N N}\right] &amp;=\sum_{i=0}^{d} \sum_{j=0}^{d} \sum_{k=0}^{c_{i n}} \operatorname{Var}[X \times F] \\ &amp;=d^{2} c_{i n} \operatorname{Var}[X] \operatorname{Var}[F] . \end{aligned}$

通过对卷积核F给定一个很小的方差作为初始化，输出特征Y的方差可以被控制为和输入特征X相似。然而在AdderNet中，输出特征的方差被计算为。

$\begin{aligned} \operatorname{Var}\left[Y_{\text {AdderNet }}\right] &amp;=\sum_{i=0}^{d} \sum_{j=0}^{d} \sum_{k=0}^{c_{\text {in }}} \operatorname{Var}[|X-F|] \\ &amp;=\sqrt{\frac{\pi}{2}} d^{2} c_{i n}(\operatorname{Var}[X]+\operatorname{Var}[F]) \end{aligned}$

可以看到，我们无法给定一个F的方差使得输出特征的方差维持不变，于是输出特征的量级会大大的高于输入的特征，如果不对其进行归一化，将会导致输出的数量级随着网络的深度爆炸。

幸运的是，现有的神经网络都使用批归一化来控制每层的特征量级相似，然而，批归一化对于AdderNet的优化会带来新的问题。给定训练批次$β={x_1,···,x_n}$ ，BN层可以被表示为：

$y=\gamma \frac{x-\mu_{\mathcal{B}}}{\sigma_{\mathcal{B}}}+\beta$

其中 和 是可学习的参数， 和 是输出特征的均值和方差。BN层的梯度被计算为：

$\frac{\partial \ell}{\partial x_{i}}=\sum_{j=1}^{m} \frac{\gamma}{m^{2} \sigma_{\mathcal{B}}}\left\{\frac{\partial \ell}{\partial y_{i}}-\frac{\partial \ell}{\partial y_{j}}\left[1+\frac{\left(x_{i}-x_{j}\right)\left(x_{j}-\mu_{\mathcal{B}}\right)}{\sigma_{\mathcal{B}}}\right]\right\}$

由于AdderNet的方差很大，计算出的偏导数的量级会很小，于是，AdderNet对滤波器的梯度将会变的很小。

表1展示了AdderNet和CNN中滤波器梯度的量级大小，可以看到，AdderNet中滤波器梯度要远远小于CNN，这将十分不利于AdderNet的训练。此外，AdderNet每一层的梯度量级都不一样，因此，我们提出了基于归一化的自适应学习率，以便于AdderNet的训练。具体的，每层的梯度被计算为：

$\Delta F_{l}=\gamma \times \alpha_{l} \times \Delta L\left(F_{l}\right)$

其中γ是整个网络的全局学习率,$\Delta L(F_{l})$ 是第l层的梯度， $α_l$是l层的学习率。由于AdderNet计算的是特征和滤波器之间的减法，它们的量级大小应该相似从而有利于特征的提取，由于每层的特征都进行了归一化，其量级都近似一样，所以每层的滤波器的量级也应该相似。基于此考虑，我们将每层的学习率计算为：

$\alpha_{l}=\frac{\eta}{\sqrt{k}\left\|\Delta L\left(F_{l}\right)\right\|_{2}}$

其中k 代表$F_l$中元素的个数，η 为控制所有adder层的超参数。通过使用这个方法，每层的滤波器可以以相同且更快的更新速度进行优化。

结果

表明，加法滤波器有望代替原始卷积滤波器用于计算机视觉任务中。